Daftar isi
Dalam matematika, ada beberapa jenis trasnformasi yaitu translasi, refleksi, rotasi, dan juga dilatasi. Translasi, rotasi, dan refleksi merupakan jenis transformasi isometri atau transformasi yang akan menghasilkan bayangan kongruen dengan asalnya. Sementara dilatasi bukan termasuk translasi isometri karena bayangan yang dihasilkan tidak kongruen namun mengubah ukuran baik memperbesar maupun memperkecil dari asalnya.
Untuk memperjelas mengenai apa itu dilatasi, maka pada pembahasan kali ini, akan diulas mengenai pengertian, sifat, rumus dan juga contoh dilatasi.
Pengertian Dilatasi
Dilatasi merupakan salah satu bentuk transformasi. Pada dilatasi transformasi yang terjadi bisa mengubah ukuran, baik itu memperbesar maupun sebaliknya yakni memperkecil, akan tetapi dilatasi tidak mengubah bentuk bangun geometri yang bersangkutan.
Dilatasi sendiri adakalanya disebut juga dengan pelebaran. Pada perhitungannya, dilatasi bisa ditentukan oleh faktor skala (k) maupun oleh titik pusat O (0.0). Adapun untuk menghitung atau menentukan dilatasi sebuah titik atau bangun geometri maka digunakan rumus dilatasi yang akan dijelaskan pada pembahasan selanjutnya.
Jadi, dilatasi bisa diartikan sebagai suatu trasnformasi yang memindahkan titik-titik pada bangun geometri yang perpindahannya tergantung pada titik pusat dilatasi dan faktor (skala) dilatasi, yang berakibat bayangan dari bangun geometri yang didilatasi akan berubah ukurannya, baik membesar ataupun mengecil.
Sifat Dilatasi
Dilatasi memiliki sifat-sifat tertentu terkait dengan besar faktor skalanya. Berikut adalah beberapa sifat dari transformassi dilatasi:
- Apabila faktor dilatasi lebih dari 1 ( k > 1), maka bayangan akan diperbesar dan terletak sepihak terhadap pusat dilatasi dan bangun asal.
- Apabila faktor dilatasi berada diantara 0 hingga 1 (0 < k < 1), maka bangun bayangan akan diperkecil dan terletak sepihak terhadap pusat dilatasi dan bangun asal.
- Apabila faktor dilatasi terletak diantara -1 hingga 0 (-1 < k < 0), maka bangun bayangan akan diperkecil dan terletak berlainan pihak terhadap pusat dilatasi dan bangun asal.
- Apabila faktor dilatasi kurang dari -1 (k < -1), maka bangun bayangan diperbesar dan terletak berlainan pihak terhadap pusat dilatasi dan bangun awal.
Contoh Dilatasi dalam Kehidupan Sehari Hari
Diantara contoh penerapan dilatasi dalam kehidupan sehari-hari adalah:
- Pada cara kerja mikroskop untuk memperbesar objek yang sangat kecil atau mikroskopis dengan faktor dilatasi atau pembesaran hingga ribuan kali.
- Pada pembuatan miniatur atau maket yang memperkecil objek asli dengan faktor skala tertentu.
- Pada pembuatan peta atau denah dengan skala tertentu.
Rumus Dilatasi
Sebagaimana telah disinggung sebelumnya bahwa perhitungan dilatasi ditentukan oleh faktor skala dan juga titik pusatnya. Dilatasi yang berpusat di P dengan faktor skala k dinotasikan dengan [P, k].
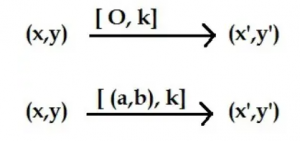
Dilatasi dengan Titik Pusat (0,0)
Dilatasi dengan titik pusat (0,0) dengan faktor skala k dinotasikan dengan [ O, k]
Untuk menghitung nilai dilatasi [O, k] dari titik asal (x,y), secara umum bisa digunakan rumus:
x’ = kx dan y’= ky
Jadi, untuk dilatasi dengan titik pusat (0,0) cara menentukan titik bayangannya cukup mudah, yaitu hanya dengan mengalikan nilai x dan y dengan faktor skala dilatasinya.
Dilatasi terhadap Titik Pusat P (a, b)
Dilatasi dengan titik pusat (a,b) dengan faktor skala k dinotasikan dengan [ (a,b), k]
Untuk menghitung nilai dilatasi [(a,b), k] dari titik asal (x,y), secara umum bisa digunakan rumus:
x’ = a + k(x – a) dan y’ = b + k(y – b)
Contoh Soal Dilatasi
1. Tentukan bayangan titik P (4,-12) yang didilatasi terhadap titik pusat (0,0) dengan faktor skala ½
Penyelesaian:
Untuk dilatasi dengan titik pusat (0,0), maka kita gunakan rumus x’ = kx dan y’= ky
Jadi untuk titik (4, -12) bayangannya adalah
x’ = kx = ½ (4) = 2
y’= ky = ½ (-12) = -6
Maka P’ (2,-6)
2. Diketahui sebuang bangun segitiga dengan titik sudut pada koordinat sebagai berikut: A(2,3), B(7,1) dan C(-2,-5). Bangun tersebut kemudian di-dilatasi dengan faktor skala 3 terhadap pusat M(1,3). Maka tentukan koordinat bayangannya!
Penyelesaian:
Untuk dilatasi dengan pusat M (1,3) dan k=3, maka kita gunakan rumus x’ = a + k(x – a) dan y’ = b + k(y – b)
A (2,3) maka koordinat bayangannya adalah:
x’ = 3(2-1) + 1 = 4
y’ = 3(3-3)+3 = 3
jadi A’ (4,3)
B (7,1) maka koordinat bayangannya adalah:
x’ = 3(7-1) + 1 = 19
y’ = 3(1-3) + 3 = -3
jadi B’ (19, -3)
C (-2,-5) maka koordinat bayangannya adalah:
x’ = 3(-2-1) + 1 = -8
y’ = 3(-5-3) + 3 = -21
jadi C’ (-8, -21)
3. Tentukan bayangan kurva y = x² – 6x + 5 jika di dilatasi dengan faktor skala 3 dan pusat (0,0).
Pembahasan:
x’ = 3x → x = 1/3 x’
y’ = 3y → y = 1/3 y’
Kemudian nilainya disubstitusikan ke persamaan y = x² – 6x + 5, maka hasilnya menjadi: 1/3 y’ = (1/3 x’)² – 6(1/3x’) + 5 1/3 y’ = (1/9 x’)² – 2x’ + 5 (Semua ruas kalikan dengan 3) y’ = (1/3x’)² – 6x’ + 15
Jadi persamaannya akan menjadi y = 1/3x2 – 6x +15
4. Sebuah titik P(- 6,4) didilatasi sehingga menghasilkan bayangan di titik P'( 3 , -2) dan pusat dilatasi (0,0). Tentukan besarnya faktor skala dilatasinya!
Pembahasan:
Untuk menentukan besarkan faktor skala dilatasi dari soal diatas, maka kita bisa berpedoman pada rumus x’ = kx dan y’= ky
x’ = kx 3 = k (-6) maka k = 3:(-6) = - ½ y’= ky -2 = k (4) maka k = (-2) : 4 = - ½
