Segitiga: Pengertian – Jenis dan Contoh Soal

√ Edu Passed Pass quality & scientific checked by advisor, read our quality control guidelance for more info
  • Review Akademik by: Review Akademik by: Sutiono M.Kom., M.T.I
  • Post author Scientific Rev by: Redaksi Haloedukasi

Dalam Bangun Datar, segitiga merupakan salah satu jenisnya. Segitiga sendiri terbagi dalam beberapa jenis. Berikut pembahasannya.

Apa itu Segitiga?

Segitiga adalah nama dari suatu bentuk tiga sisi berupa garis lurus dan tiga sudut.

Pada tahun sekitar 300 SM seorang matematikawan bernama Euclid menemukan jumlah ketiga sudut pada suatu segitiga datar (180 derajat).

Segitiga sendiri adalah bangun datar yang saling berpotongan. Dibentuk oleh tiga buah titik sudut yang letaknya tidak segaris dan dihubungkan.

Jenis-jenis Segitiga dan Rumusnya

Berikut ini adalah jenis-jenis dari segitiga yang perlu diketahui, antara lain:

Menurut Panjang Sisinya

Menurut panjang sisinya, segitiga mempunyai beberapa jenis, antara lain:

1. Segitiga Sama Sisi (Equaliteral Triangle)

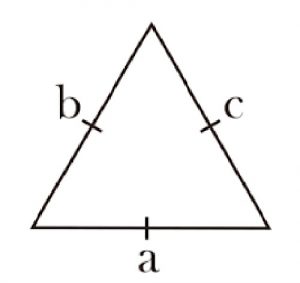
Segitiga

Segitiga ini merupakan segitiga dengan semua sisinya (ketiga sisinya) memiliki panjang yang sama.

Sehingga, jenis segitiga ini semua sudutnya sama besar (60 derajat).

Sifat Segitiga Sama Sisi

  • Mempunyai tiga buah sisi yang sama panjang.
  • Mempunyai tiga buah sudut yang sama besar.
  • Mempunyai tiga sumbu yang simetri.

Rumus Segitiga Sama Sisi

  • Luas
L = ½ a x t
  • Tinggi
t = ½ x a x √3
  • Keliling
K = sisi1 + sisi2 + sisi3

Keterangan:
K = keliling segitiga
a = panjang sisi segitiga

2. Segitiga Sama Kaki (Isosceles Triangle)

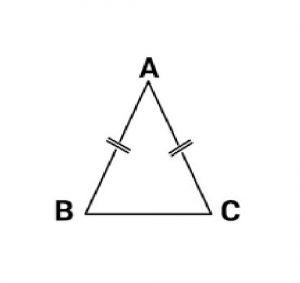
Segitiga

Segitiga ini merupakan segitiga yang dua sisinya mempunyai panjang yang sama sehingga segitiga ini memiliki dua sudut yang sama besarnya.

Sifat Segitiga Sama Kaki

  • Memiliki dua buah sisi yang sama panjang (kakinya)
  • Memiliki satu buah sumbu yang simetri
  • Memiliki dua sudut yang besar (sudut yang berhadapan dengan sisi yang sama panjang)

Rumus Segitiga Sama Kaki

  • Keliling
Keliling = sisi x + sisi y +sisi z
  • Luas
L = ½ a x t

Keterangan:
a = alas
t = tinggi

3. Segitiga Sembarang (Scalene Triangle)

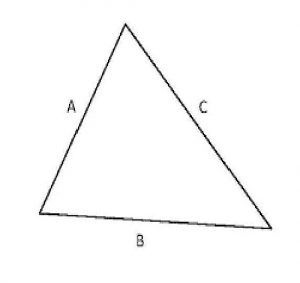
Segitiga

Segitiga ini merupakan segitiga yang memiliki sisi yang panjangnya berbeda di setiap sisinya. Sehingga semua sudutnya juga sama besar.

Sifat Segitiga Sembarang

  • Mempunyai tiga sisi yang tidak sama-sama panjang.
  • Mempunyai tiga buah sisi yang tidak sama-sama panjang.
  • Tidak memiliki simetri yang lipat.
  • Mempunyai simetri yang putar hanya satu buah.
  • Semua sudut (ketiga-tiganya) mempunyai besar yang berbeda.

Rumus Segitiga Sembarang

  • Luas
L = √(s(s-a)(s-b)(s-c)
  • Keliling
K = (a+b+c)/2

Keterangan:
L= Luas
K= Keliling
S= Sisi

Menurut Besar Sudutnya

Menurut besar sudut terbesarnya, segitiga mempunyai beberapa jenis, antara lain:

1. Segitiga Siku-siku

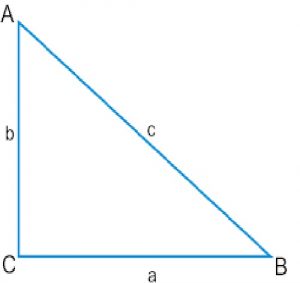
Segitiga

Segitiga ini merupakan segitiga yang salah satunya mempunyai besar sudut 90 derajat.

Sisi di depan sudut 90 derajat dinamakan dengan hipotenusa atau sisi miring.

Sifat Segitiga Siku-siku

  • Memiliki dua sisi yang saling tegak lurus.
  • Mempunyai satu sisi miring dan salah satu sudutnya adalah siku-siku.
  • Memiliki dua simetri (simetri lipat dan simetri putar).

Rumus Segitiga Siku-siku

  • Luas
L = ½ x alas x tinggi
  • Keliling
K= sisi1 + sisi2 + sisi3

Keterangan:
L = Luas
K= Keliling

2. Segitiga Lancip

Segitiga

Segitiga ini merupakan segitiga yang semua sudutnya sama-sama besar, yaitu kurang dari 90 derajat.

Sifat Segitiga Lancip

  • Ketiga sudut merupakan sudut lancip (besar sudut antara 0ᵒ dan 90ᵒ) dengan jumlah 180ᵒ.
  • Kuadrat dalam sisi terpanjang lebih kecil daripada jumlah kuadrat sisi lain (c² < a² + b², dengan c adalah sisi terpanjang) Total dua buah sisi segitiga selalu lebih besar dari panjang sisi lain (a + b > c, a + c > b dan b + c > a)

Rumus Segitiga Lancip

  • Keliling
K = a + b + c
  • Luas
L = 1/2 x alas x tinggi

Keterangan:
K = keliling
L= Luas

3. Segitiga Tumpul

Segitiga

Segitiga ini merupakan segitiga dengan salah satu sudut sebesar 90 derajat.

Sifat Segitiga Tumpul

  • Salah satu sudutnya ada yang lebih dari 180 derajat.
  • Memiliki dua sudut yang sama besar.
  • Memiliki dua sisi yang sama panjang.
  • Memiliki dua sudut yang sama-sama 90 derajat.

Rumus Segitiga Tumpul

  • Luas
L= 1/2 x a x t
  • Keliling
K= 2 x (P+L)

Keterangan:
K= Keliling
L= Luas

Contoh Soal Segitiga

1. Terdapat sebuah segitiga dengan panjang alas 30 cm memiliki luas 185 cm2. Hitung tinggi dari segitiga tersebut!

Jawab:

½ x alas x tinggi 
185 = 1/2 x 30 x tinggi
185 = 15 x tinggi
Tinggi = 185:15
Tinggi = 12,3 cm

Jadi, tinggi segitiga tersebut adalah 12,3 cm.

2. Panjang sisi 1=5 cm, sisi 2=7 cm, dan sisi 3=9 cm, serta tinggi segitiga = 9 cm. Hitunglah keliling dari segitiga ini.

Jawab:

K= (sisi 1+sisi 2+sisi 3)
K= 5 + 7 + 9
K= 23 cm

Jadi, Keliling segitiga tersebut adalah 23 cm.

3. Segitiga sama sisi mempunyai panjang kaki sebesar 12 cm. Hitunglah tinggi dari segitiga di atas!

Jawab:

L = ½ alas x tinggi
Alas = 12 cm
Dalam menghitung tinggi segitiga, dibutuhkan rumus Teorema Pythagoras, yaitu c2=a2+b2.
122= a2+b2
122= 62+b2
144= 36+b2
B2= 144-36
B2= 108
Akar dari 108= 10,4 cm

Jadi, tinggi dari segitiga tersebut adalah 10,4 cm

fbWhatsappTwitterLinkedIn

Related Posts