Daftar isi
Pada kali ini kita akan belajar mengenai komposisi fungsi dan invers disertai soal dan pembahasan yang akan mempermudah dalam pemahaman materi ini.
Untuk mempelajari materi ini Anda harus terlebih dahulu paham mengenai materi relasi dan fungsi. Simak pembahasannya dibawah ini.
Pengertian fungsi
Fungsi adalah aturan yang menghubungan anggota himpunan A dengan anggota himpunan B.
Suatu relasi dikatakan fungsi apabila setiap anggota himpunan A dipasangkan tepat satu anggota himpunan B.
Jika f adalah suatu fungsi dari A ke B maka himpunan A disebut daerah asal (domain), himpunan B daerah kawan (kodomain), dan himpunan B yang berpasangan disebut hasil (range).
Jenis-jenis Fungsi
1. Fungsi Linear
Fungsi linear adalah suatu fungsi yang memiliki 2 variabel atau lebih yang variabel bebasnya memiliki pangkat tertinggi nya satu.
Bentuk umum fungsi linear : f(x) = ax + b, a dan b konstan dengan a ≠ 0
2. Fungsi Konstan
Fungsi yang dinyatakan dengan rumus f(x) = c, dengan c merupakan konstanta
3. Fungsi Identitas
Fungsi identitas adalah fungsi dari A ke B jika dan hanya jika range f = kodomain atau f(A)=B
Fungsi kuadrat yaitu fungsi yang dinyatakan dengan rumus f(x) = ax2 + bx + c, di mana a ≠ 0 dan a, b, dan c bilangan konstan.
Komposisi Fungsi
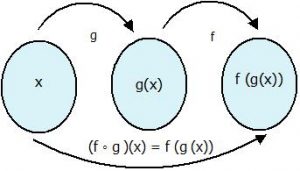Sebuah fungsi yang digabungkan ke dalam fungsi lain sehingga menghasilkan fungsi baru itu disebut komposisi fungsi.
(f ◦ g )(x) = f (g (x)) ; komposisi g ( fungsi komposisi dengan g dikerjakan lebih dahulu daripada f)
Suatu fungsi g digabungkan dengan fungsi f
(g ◦ f )(x) = g (f (x)) ; komposisi f ( fungsi komposisi dengan f dikerjakan lebih dahulu daripada g)
Suatu fungsi f digabungkan dengan fungsi g
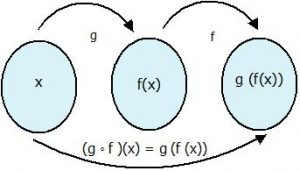
Untuk mempermudah pemahaman mengenai menghitung komposisi fungsi, simak diagram disamping.
Sifat-sifat Komposisi Fungsi:
- Tidak berlaku sifat komutatif
- Bersifat asosiatif , (f ◦ ( g ◦ h ))(x) = (( f ◦ g )◦ h)(x)
- Terdapat unsur identitas (I)(x) , (f ◦ I)(x) = (I ◦ f)(x) = f(x)
Invers Fungsi
Invers fungsi adalah fungsi yang membalikkan dari suatu fungsi. Jika suatu f fungsi yang memetakan x ke y, maka invers dari f yaitu f –1 akan memetakan y ke x.
Dengan kata lain bahwa daerah hasil dari f-1 (x) merupakan daerah asal bagi f(x) begitupun sebaliknya.
Invers Fungsi Komposisi
Invers fungsi komposisi yaitu invers dari gabungan dua buah fungsi ataupun lebih.
Jika h(x) = (g ◦ f) (x) maka invers fungsi komposisi nya h-1 = (g ◦ f)-1 (x) ; h-1 = (f-1 ◦ g-1) (x)
Contoh Soal dan Pembahasan
1. Diketahui sebuah fungsi f(x) = 2x + 1 dan g(x) = x2 + 1 tentukan (g ◦ f) (x) dan (f ◦ g) (x)
Jawab:
(g ◦ f)(x) = g(f (x)) = g(2x +1) = (2x + 1)2 + 1 (g ◦ f)(x) = 4x2 + 4x + 1
Sedangkan untuk mencari (f ◦ g)(x)
(f ◦ g)(x) = f(g (x)) = f( x2 + 1 ) = 2 ( x2 + 1 ) + 1 (f ◦ g)(x) = 2x2 + 2 + 1 = 2x2 + 3
2. Diketahui sebuah fungsi f(x) = 2x + 4 dan g(x) = x2 – 1 tentukan (g ◦ f) (2) dan (f ◦ g) (2)
Jawab:
Hitung dahulu (g ◦ f) (x) dan (f ◦ g) (x)
(g ◦ f)(x) = g(f (x)) = g(2x + 4) = (2x + 4)2 - 1 (g ◦ f)(x) = 4x2 + 16x + 16
Sedangkan untuk mencari (f ◦ g)(x)
(f ◦ g)(x) = f(g (x)) = f( x2 - 1 ) = 2 ( x2 + 1 ) + 4 (f ◦ g)(x) = 2x2 + 2 + 4 = 2x2 + 6
Maka (g ◦ f) (2) dan (f ◦ g) (2)
(g ◦ f)(2) = 4.22 + 16.2 + 16 (g ◦ f)(2) = 16 + 32 + 16 = 64
Sedangkan (f ◦ g)(2) (f ◦ g)(2) = 2.22 + 2 + 4 = 2.22 + 6 (f ◦ g)(2) = 8 + 6 = 14