Daftar isi
Pada pembahasan kali ini, yang akan kita bahas mengenai pengertian relasi, cara menyatakan relasi, fungsi, banyaknya fungsi, korespondensi satu-satu. Untuk lebih jelasnya simak pembahasannya dibawah ini.
Relasi
Pengertian Relasi
Relasi adalah hubungan antara daerah asal (domain) dan daerah kawan (kodomain).
Misalkan relasi dari himpunan A ke himpunan B yaitu memasangkan atau korespondensi anggota himpunan A ke anggota himpunan B dengan aturan tertentu.
Cara menyatakan Relasi
Dalam menyatakan relasi, ada 3 caa yaitu:
1. Diagram Panah
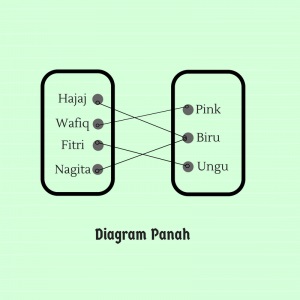
Gambar diatas menunjukkan relasi warna yang disukai dari sebuah himpunan A ke himpunan B.
Dimana arah panah menunjukkan anggota himpunan A yang berelasi dengan anggota himpunan B.
Langkah-langkah untuk menyatakan relasi dengan diagram panah:
- Membuat lingkaran atau elips (banyaknya lingkaran sesuai dengan banyaknya himpunan)
- Tuliskan anggota himpunan A dan anggota himpunan B pada masing-masing lingkaran ( misal anggota himpunan A diletakkan pada lingkaran X dan anggota himpunan B diletakkan pada lingkaran Y)
- X dan Y dihubungkan dengan anak panah ataupun garis
- Anak panah atau garis itu mewakili aturan relasi.
2. Diagram Cartesius
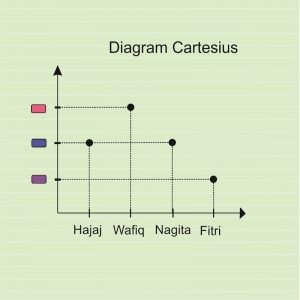
Gambar diatas menunjukkan relasi himpunan A ke himpunan B dengan cara diagram cartesius.
Dimana anggota-anggota himpunan A berada pada sumbu mendatar sedangkan anggota-anggota himpunan B berada pada sumbu tegak.
Setiap himpunan yang berelasi kita nyatakan dengan menggunakan titik atau noktah.
Langkah-langkah untuk menyatakan relasi dengan diagram cartesius:
- X merupakan himpunan A dan di letakkan pada sumbu mendatar
- Y merupakan himpunan B dan diletakkan pada sumbu tegak
- Pemasangan (X,Y) ditandai dengan sebuah titik atau noktah yang koordinatnya ditulis sebagai pasangan berurut (X,Y.
3. Himpunan Pasangan Berurut
Himpunan yang anggotanya semua pasangan berurutan (X,Y) dinamakan himpunan pasangan berurutan.
Fungsi (Pemetaan)
Pengertian Fungsi
Fungsi adalah aturan yang menghubungkan anggota himpunan A dengan anggota himpunan B.
Suatu relasi dikatakan fungsi apabila setiap anggota himpunan A dipasangkan tepat satu anggota himpunan B.
Jika f adalah suatu fungsi dari A ke B maka himpunan A disebut daerah asal (domain), himpunan B daerah kawan (kodomain), dan himpunan B yang berpasangan disebut hasil (range).
Untuk nama suatu fungsi pada umumnya adalah f, g, atau hurup lainnya.
Misal diketahui fungsi:
f: A → B ditentukan dengan notasi f(x) g: C → D ditentukan dengan notasi g(x).
Cara membaca fungsi, misalkan f(x) di baca “ f dari x “ menunjukkan nilai yang diberikan oleh f kepada x.
Contoh Soal dan Pembahasan
1. Tuliskan domain, kodomain, dan range dari diagram panah diatas!
Jawab:
Domain = {Hajaj, Wafiq, Nagita, Fitri}
Kodomain = {Pink, Biru, Ungu}
Range = {Pink, Biru, Ungu}
Banyaknya fungsi:
Banyaknya anggota himpunan A disebut n(A) dan banyaknya anggota himpunan B disebut n(B).
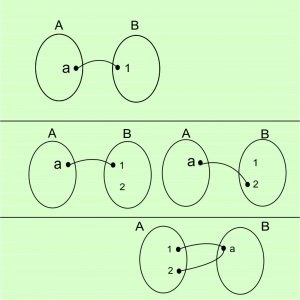
Jika A = {a} dan B = {1} semua pemetaan yang mungkin dari A ke B adalah (a , 1).
n(f : A -> B) = 11 = 1 buah
Jika A = {a} dan B = {1 , 2} semua pemetaan yang mungkin dari A ke B adalah (a , 1), (a , 2).
n(f : A -> B) = 21 = 2 buah
Jika A = {a} dan B = {1 , 2} semua pemetaan yang mungkin dari B ke A
n(f : A -> B) = 11 = 1 buah
Untuk menentukkan banyaknya fungsi digunakan rumus :
- Banyak pemetaan dari A ke B = n(B)n(A)
- Banyak pemetaan dari B ke A = n(A)n(B).
