Bilangan bulat merupakan salah satu pembahasan penting dalam mata pelajaran matematika khususnya dan umumnya dalam praktek kehidupan, kenapa begitu? Salah satu contoh fungsinya dalah kehidupan diantaranya bagaimana kita membilang banyak benda. Banyak benda tersebut dinyatakan dengan bilangan 0,1,2,3 dan seterusnya. Bilangan semacam ini disebut sebagai bilangan cacah. (baca juga : Pengertian Bilangan Prima)
Namun ternyata semua keadaan tidak bisa diwakili hanya dengan bilangan cacah di atas, misalnya bagaimana kita mengatakan posisi burung yang hinggap di puncak tiang kapal setinggi 3 meter di atas laut, dan posisi nelayan yang sedang menyelam di kedalaman 3 meter di bawah laut? Posisi tersebut dapat kita gambarkan sebagai berikut burung yang hinggap di atas tiang berada 3 meter di atas permukaan laut atau dilambangkan +3, biasanya diringkas dengan bilangan 3.
Sedangkan posisi nelayan yang berada di kedalama 3 metert dapat dilambangkan dengan -3. Dalam ilmu matematikan bilangan +3 atau 3 biasa disebut dengan positif tiga dan bilangan -3 dibaca negatif tiga. Ilustrasi tersebut dapat digambarkan dalam dalam garis vertikal dan horizontal sebagai berikut:
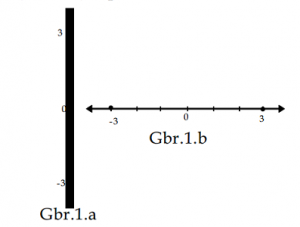
Gambar di samping mewakili permisalahan sebagai dijelaskan di atas yaitu bahwa garis horizontal mewakili permukaan laut dan garis vertikal mewakili tinggi dari burung yang hinggap dan kedalaman pelaut yang sedang menyelam.
Dengan demikian yang diimaksud dengan bilangan bulat adalah bilangan cacah yang selalu memiliki nilai positif atau disebut bilangan cacah positif dimulai dari 0,1,2,3 dan seterusnya.
Dan bilangan cacah yang memilki nilai negatif atau bilangan negatif dimulai dari -1,-2.-3 dan seterusnya. Jadi ada dua macam dari bilangan bulat yaitu bilangan bulat positif dan bilangan bulat negatif
Perlu diperhatikan bahwa -0 = 0 . Oleh karena itu tidak ada permisalan untuk negatif nol dari bilangan cacah!
Membandingkan dan Mengurutkan Bilangan Bulat
Dalam mata pelajaran matematika ada beberapa hal yang dipelajari dari bilangan bulat, salah satunya adalah membandingkan bilangan bulat. Masih ingatkah? Untuk memanggil kembali memori anda perhatikan gambar dan pertanyaan berikut:
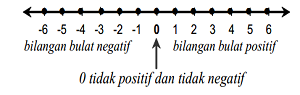
Gambar di disamping adalah bentuk himpunan dari bilangan bulat, pengertian himpunan sendiri adalah suatu kelompok yang anggotanya memiliki suatu kesamaan sehingga bisa dibedakan dengan kelompok lainnya.
Pada gambar di atas perhatikan 3 dan 5. Lebih besar mananakah antara bilangan 3 dan 5 tersebut, bilangan mana yang lebih panjang?
Ingat bahwa pada suatu garis bilangan sebagaimana gambar di atas bahwa setiap bilangan yang terletak di kiri selalu kurang dari bilangan yang terletak disebelah kananya. Oleh karena itu rumus dari membandingkan dan mengurutkan bilangan adalah sebagai beikut:
Jadi jawaban dari persoalan di atas adalah 3 lebih kecil dari 5. Namun dalam mata pelajaran matematika ada beberapa simbol mengenai perbandingan sebuah bilangan bulat sebagaimana dijelaskan pada gambar di samping.
Jadi untuk membandingkan bilangan bulat pada ilmu matematika tidak menggunakan kata-kata dalam menyatakan besar perbandingan dari bilangan bulat akan tetapi menggunakan permisalan atau simbol sebagaimana dijelaskan pada gambar di samping berupa simbol sama dengan, kurang dari dan lebih dari.
Oleh karena itu permisalan untuk 3 lebih kecil dari pada 5 adalah 3 < 5.
[AdSense-A]
Operasi dari Bilangan Bulat
Operasi bilangan bulat yang dimaksud adalah bagaimana cara kita mengaplikasikan bilangan bulat sesuai dengan panduan dari ilmu matematika. Ada 4 (empat) macam operasi dari bilangan bulat dalam ilmu matematika, operasi tersebut adalah sebagai berikut:
1. Penjumlahan
Dalam sistem penjumlahan bilangan bulat ini setiap penjumlahan dari bilangan bulat memiliki sifat-sifatnya tersendiri, sifat tersebut antara lain:
- Tertutup
Setiap menjumlahkan 2 (dua) bilangan atau lebih maka hasilnya akan selalu bilangan bulat.
Contoh: 1 + 3 = 4, jadi 4 merupakan bilangan bulat
- Komutatif
Setiap penjumlahan bilangan bulat meskipun posisinya ditukar hasilnya akan tetap sama.
a + b = b + a
Contoh : 1 + 3 = 3 + 1
- Asosiatif
Setiap penjumlahan bilangan bulat yang dikelompokkan dalam posisi yang berbeda hasilnya akan tetap sama.
(a + b) + c = a + (b +c)
Contoh : (1 + 3) + 2 = 1 (3 + 2)
- Unsur identitas
Maksudnya adalah jika bilangan bulat dijumlahkan dengan nol maka hasilnya akan tetap.
Contoh : 1 + 0 = 1
- Invers
Maksudnya adalah penjumlahan bilangan yang berlawanan makan hasilnya akan nol.
Contoh : 5 + (-5) = 0
2. Pengurangan
Gambar disamping merupakan ilustrasi pengoperasian penguranagn bilangan bulat dengan cara mengambar garis bilangan terlebih dahulu.
Berbeda halnya dengan penjumlahan, dalam pengurangan apabila bilangan dikurangkan maka hasilnya tidak bisa bersifat tertutup sebagaimana penjumlahan. Artinya sifat dari pengurangan bilangan bulat adalah tidak tertutup dan tidak komutatif.
Contoh : 7 – 3 = 4 bila kemudian dibalik 3 – 7 = -4
Jadi jika dibalik, maka hasil dari pengurangan bukanlah bilangan cacah akan tetapi bilangan negatif.
[AdSense-C]
3. Perkalian
Aturan baku pada perkalian bilangan bulat adalah sebagaimana di tampilkan pada gambar disamping. Hampir menyerupai penjumlahan perkalian juga mempunyai beberapa sifat. Sidat-sifat tersebut menentukan bagaimana operasi perkalian bilangan bulat, setiap sifat tersebut berpengaruh pada hasil dari perkalian bilangan bulat.
Adapun sifat-sifat tersebut adalah sebagai berikut:
- Tertutup
Artinya semua bilangan dalam perkalian sifatnya tertutup
Contoh: 4 x 2 = 8
- Komutatif
Artinya dalam perkalian bilangan bulat apabila ditukat hasilnya akan tetap sama
a x b = b x a
Contoh : 2 x 3 = 3 x 2
- Distibutif
Yakni sifat penyebaran perkalian terhadap pembagian
( a x b) + ( a x c) = a x (b + c)
Contoh :
( 2 x 3) + ( 2 x 4) = 2 x (3 + 4)
- Unsur identias
Semua bilangan apabila dikalingan 1 (satu) hasilnya akan tetap sama.
a x 1 = 1 x a = a
Contoh:
4 x 1 = 1 x 4 = 4
4. Pembagian
Dalam pembagian bilangan bulat sifat dari bilangan adalah tidak tertutup.
Contoh :
11 : 5 = 2 ½
Demikianlah uraian mengenai pengertian bilangan bulat sekaligus operasi bilangan bulat yang semoga tulisan ini bisa membantu anda dalam memahami secara lebih jelas mengenai bilangan bulat.