Persamaan Garis Lurus: Pengertian – Rumus dan Contoh Soal

√ Edu Passed Pass quality & scientific checked by advisor, read our quality control guidelance for more info
  • Review Akademik by: Review Akademik by: Sutiono M.Kom., M.T.I
  • Post author Scientific Rev by: Redaksi Haloedukasi

Materi yang akan kita pelajari yaitu pengertian, menentukan gradien suatu garis, rumus, dan contoh soal untuk mempermudah pemahaman tentang persamaan garis lurus. Simak pembahasan nya dibawah ini.

Pengertian Persamaan Garis Lurus

persamaan garis lurus

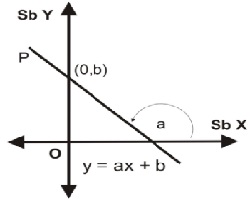
Persamaan garis lurus adalah suatu garis lurus yang kedudukannya ditentukan oleh suatu persamaan.

Atau suatu perbandingan antara koordinat x dan koordinat y dari dua titik yang terletak pada garis.

Gradien Garis Lurus

Gradien adalah kemiringan suatu garis terhadap sumbu X atau perbandingan komponen Y dan X.

Gradien biasa dinotasikan dengan huruf “m”. Bentuk umum persamaan adalah y = mx + c, dengan m adalah gradien dan c adalah konstanta.

  • Gradien dengan persamaan ax + by + c = 0 , maka m = komponen x/komponen y
  • Gradien yang melalui titik pusat ( 0 , 0 ) dan titik ( a , b ), maka m = b/a
  • Gradien yang melalui titik  ( x1, y1 ) dan ( x2, y2 ) , maka m = y1 – y2 / x1 – x2 atau m = y2 – y1 / x2 – x1
  • Gradien garis sejajar, maka m = sama  atau m1 = m2
  • Gradien garis yang tegak lurus, maka m = -1 atau  m1 x m2 = -1.

Menentukan Persamaan Garis Lurus

Untuk menentukannya, kita gunakan bentuk umum yaitu y = mx + c. Untuk menentukan diperlukan hanya gradien dan konstana, yaitu dengan cara :

  • Menentukan gradien
    Dengan cara membagi delta y dengan delta x
  • Menentukan konstanta
    Dengan cara mensubstitusikan salah satu titik yang dilewati.

Contoh Soal dan Pembahasan

1. Tentukan persamaan garis lurus yang mempunyai gradien 3 dan melewati titik (5, 8)!

Jawab:

Misalkan persamaan garisnya y = mx + c,

  • Langkah pertama tentukan gradien.

Karena gradien telah diketahui yaitu m = 3 maka persamaan garisnya menjadi y = 3x + c

  • Langkah kedua tentukan konstanta (c)

Karena diketahui pada soal garis tersebut melewati titik (5, 8) maka

y = 3x + c disubstitusikan 8 = 3(5) + c

8 = 15 + c maka 8 – 15 = c , nilai konstanta ditemukan yaitu -7

jadi persamaan garisnya adalah y = 3x – 7 atau 3x – y = 7

2. Tentukan persamaan garis yang melalui titik (3 , 5) dan (4, 8) !

Jawab:

Misal persamaan garisnya adalah y = mx + c.

  • Langkah pertama tentukan gradien.
m = y1 – y2 / x1 – x2 atau m = y2 – y1 / x2 – x1
m = 5 - 8 / 3 - 4
m = 3
  • Langkah kedua tentukan konstanta (c)

Karena diketahui pada soal garis tersebut melewati titik (3, 5) maka

y = 3x + c
5 = 3(3) + c
5 = 9 + c
c = 5 - 9 = -4

Jadi persamaan garisnya adalah y = 3x – 4 atau 3x – y = 4

Untuk membuktikan kebenarannya hitung dengan menggunakan garis (4, 8) persamaannya haruslah sama karena diketahui pada soal garis tersebut melewati titik (4, 8) maka

y = 3x + c
8 = 3(4) + c
8 = 12 + c
c = 8 - 12 = -4

Jadi persamaan garisnya adalah y = 3x – 4 atau 3x – y = 4

fbWhatsappTwitterLinkedIn

Related Posts