Deret dalam ruang lingkup matematika diartikan sebagai jumlah dari barisan suatu bilangan dengan pola tertentu. Jenis deret yang terkenal dalam matematika adalah deret Aritmatika dan deret Geometri. Namun ada lagi jenis deret dalam matematika yang mungkin belum diketahui banyak orang yaitu Deret Teleskopik.
Apa sih sebenarnya deret teleskopik itu? Selengkapnya akan kita bahas pada ulasan berikut.
Apa itu Deret Teleskopik?
Apa yang terpikirkan ketika mendengar kata teleskopik? Mayoritas orang akan mulai mengaitkannya dengan suatu benda yang bernama teleskop. Dan ternyata penamaan jenis deret ini punyai kaitan dengan teleskop lho.
Coba perhatikan bentuk batang teleskop yang besar di bagian atas dan kecil di bagian bawah. Karakteristik inilah yang diambil untuk menamai deret dimana nilai suku-sukunya semakin naik atau ada juga yang semakin turun.
Secara sederhana, deret teleskopik dapat diartikan sebagai suatu deret yang suku-sukunya akan saling menghilangkan karena adanya operasi perhitungan yang saling berlawanan. Nama lain dari deret teleskopik ini adalah deret berjatuhan. Ada suatu teknik dalam memunculkan deret teleskopik yang dikenal dengan nama prinsip teleskopik.
Prinsip Deret Teleskopik
Pada bagian sebelumnya sudah dijelaskan bahwa deret ini akan meunculkan proses penghilangan suatu bilangan karena tandanya yang berlawanan. Prinsip ini dapat terlihat pada penyelesaian persoalan matematika berikut,
2022 + 2020 + 2018 + 2016 + ... + 2 + 0 - 2 - 4 - ... 2016 - 2018 - 2020
Jika dilihat sekilas, perhitungan di atas akan memakan waktu yang lama untuk penyelesaiannya. Bayangkan saja, kita diminta melakukan perhitungan dengan bilangan yang mencapai 2022. Namun sebenanrya persoalan ini sangat mudah diselesaikan jika sudah mengenal prinsip teleskopik. Lalu bagaimana sih cara penyelesaiannya?
- Pertama, coba kelompokkan suku-suku yang saling menghilangkan. Suku-suku ini ditandai dengan bilangannya sama namun tandanya berlawanan. Sehingga akan diperoleh,
2022 + (2020 - 2020) + (2018 - 2018) + ... (2 - 2) + 0
- Selanjutnya perhatikan bahwa nilai yang ada di dalam tanda kurung () akan saling menghilangkan alias menghasilkan nilai 0.
- Ada bilangan yang tidak memiliki pasangan dengan tanda yang berlawanan yaitu bilangan 2022.
- Jadi, jawabannya sudah ketemu yaitu 2020.
Contoh Soal Deret Teleskopik
Ada banyak soal yang dapat diselesaikan menggunakan prinsip teleskopik. Berikut disajikan beberapa contoh soal deret teleskopik disertai dengan pembahasan lengkapnya.
Soal 1
Tentukan nilai dari perhitungan matematika berikut!

Pembahasan:
Kebanyakan siswa ketika dihadapkan dengan soal ini akan pusing terlebih dahulu. Jika soal ini dikerjakan secara manual tentunya akan memakan waktu yang cukup lama. Tapi jika sudah menerapkan prinsip teleskopik maka hanya butuh waktu 5-10 detik saja untuk sudah mengetahui hasilnya.
Perhatikan bahwa pembilang dan penyebut pada bilangan tersebut akan saling menghilangkan. Penyebut pada bilangan pertama dengan pembilangan pada bilangan kedua dapat saling menghilangkan. Begitu juga dengan bilangan-bilangan berikutnya. Lebih jelasnya perhatikan perhitungan berikut.
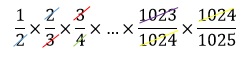
Setelah dicoret karena penyebut dan pembilang saling menghilangkan, maka tersisa pembilang pada bilangan pertama yaitu 1, dan pecahan di bilangan terakhir yaitu 1025. Jadi, jawabannya adalah 1/1025.
Soal 2
Tentukan nilai dari perhitungan matematika berikut!

Pembahasan:
Penyelesaian permasalahan pada soal dapat dilakukan dengan menyederhanakan setiap perhitungan pada tanda kurung, sehingga diperoleh
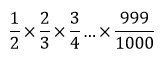
Selanjutnya, kita tinggal menggunakan prinsip teleskopik dengan cara mencoret pembilang dan penyebut yang sama.

Setelah dilakukan pencoretan bilangan yang sama maka diperoleh hasil perhitungan yaitu 1/1000.
