Daftar isi
Pernahkah kamu bermain ke tepi pantai dan memperhatikan gelombang laut? ya itu adalah gelombang stasioner tetap atau mengalami pemantulan ujung bebas. Sudah kebayang kan? Mari kita simak penjelasannya yang lebih detail lagi.
Pengertian Gelombang Stasioner
Dalam fisika, gelombang stasioner, juga dikenal sebagai gelombang berdiri, adalah gelombang yang berosilasi dalam waktu tetapi amplitudo puncaknya tidak bergerak di ruang udara.
Amplitudo puncak osilasi gelombang pada setiap titik di ruang konstan dengan waktu, dan osilasi pada titik yang berbeda di seluruh gelombang berada dalam fase.
Lokasi di mana nilai absolut dari amplitudo minimum disebut node, dan lokasi di mana nilai absolut dari amplitudo maksimum disebut antinode.
Gelombang stasioner pertama kali diperhatikan oleh Michael Faraday pada tahun 1831.
Faraday mengamati gelombang berdiri pada permukaan cairan dalam wadah bergetar.
Franz Melde menciptakan istilah “gelombang berdiri” sekitar 1860 dan mendemonstrasikan fenomena tersebut dalam eksperimen klasiknya dengan string bergetar.
Fenomena ini dapat terjadi karena media bergerak dalam arah yang berlawanan dengan gelombang, atau dapat muncul dalam medium yang tidak bergerak sebagai akibat dari gangguan antara dua gelombang yang bergerak dalam arah yang berlawanan.
Penyebab paling umum dari gelombang berdiri adalah fenomena resonansi, di mana gelombang berdiri terjadi di dalam resonator karena gangguan antar gelombang yang dipantulkan bolak-balik pada frekuensi resonansi resonator.
Jenis-jenis Gelombang Stasioner
Gelombang Stasioner terdiri atas 2 tipe, yaitu Gelombang Stasioner Bebas dan Gelombang Stasioner Terikat. Berikut penjelasannya.
1. Gelombang Stasioner Ujung Bebas (Longitudinal)
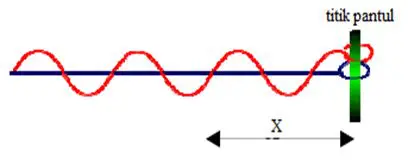
Gelombang ini dihasilkan karena gangguan dua gelombang progresif longitudinal identik berjalan di sepanjang jalur yang sama tetapi dengan tepat ke arah yang berlawanan.
Gelombang Stasioner Ujung Bebas merupakan super posisi gelombang pada seutas tali dimana salah satu ujungnya di kaitkan dengan sebuah cincin yang juga dapat bergerak bebas.
Pada gelombang jenis ini, gelombang pantul tidak mengalami pembalikan fase.
Jadi, jika sebuah gelombang tersebut tegak yang terjadi di dalam sebuah tali, maka akan terdapat titik simpul di ujung tetap, dan titik perut di ujung bebas.
Hasil superposisi gelombang datang dan gelombang pantul pada ujung bebas adalah:
y = y1 + y2.
Dengan :
y1 = A sin (kx – ωt) dan y2 = -A sin (kx + ωt)
Maka :
y = 2A cos kx sin ωt
Keterangan :
y = Simpangan gelombang stasioner (m)
x = Jarak suatu titik dari titik pantul (m)
k = Bilangan gelombang (m-1)
ω = Kecepatan sudut gelombang (rad/s)
2. Gelombang Stasioner Ujung Tetap (Transversal)
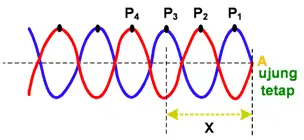
Gelombang ini dihasilkan karena gangguan dua identik gelombang progresif melintang yang bepergian di sepanjang jalur yang sama tetapi justru berbalik arah.
Gelombang Stasioner Ujung Tetap yaitu merupakan super posisi gelombang pada seutas tali dimana salah satu ujungnya di ikat pada tiang sehingga tidak dapat bergerak bebas.
Pada gelombang jenis ini, gelombang pantul mengalami pembalikan fase sebesar ½ .
Jadi, jika sebuah gelombang tegak yang terjadi di dalam sebuah tali, maka akan terdapat titik simpul di ujung tetap, dan titik perut di ujung terikat.
Hasil superposisi gelombang datang dan gelombang pantul pada ujung bebas adalah:
y = y1 + y2.
Dengan :
y1 = A sin (ωt – kx) dan y2 = -A sin (ωt + kx)
Maka :
y = 2A sin kx cos ωt
Keterangan:
y = Simpangan gelombang stasioner (m)
x = Jarak suatu titik dari titik pantul (m)
k = Bilangan gelombang (m-1)
ω = Kecepatan sudut gelombang (rad/s)
Contoh Soal dan Pembahasan
Soal 1
Suatu gelombang yang frekuensinya 500 Hz merambat dengan kecepatan 300 m/s. tentukan jarak antara dua titik yang berbeda sudut fase 60o!
Jawaban:
Diketahui:
f = 500 Hz
v = 300 m/s
∆θp = 60o
Ditanya: ∆x =…?
Pembahasan:
Pertama, Quipperian harus menentukan panjang gelombangnya.
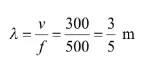
Lalu, gunakan rumus beda fase berikut.
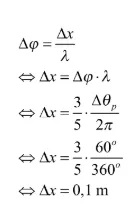
Jadi, jarak antara dua titik yang berbeda sudut fase 60o adalah 0,1 m.
Soal 2
Panjang tali (l) = 10m
Ujung terikat
A = 10 cm
f = 5Hz
v = 5 m/s
Jawaban :
v = λf
5 = λ 5
λ = 1m
Ap = 2A sin kx
Ap = 2 A sin 2 pi x/ λ
Ap = 2 10 sin 2 pi 2 / λ
Ap = 2 10 0
Ap = 0 m
Jadi amplitude padajarak 2 m di titik P adalah 0 m. Keadaan itu berarti amplitude pada keadaan simpul gelombang yang menjadikan nilai amplitude di titik P bernilai 0
Soal 3
Ujung sebuah tali yang panjangnya 1 meter di getarkan sehingga dalam waktu 2 sekon terdapat 2 gelombang. Tentukanlah persamaan gelombang tersebut apabila amplitudo getaran ujung tali 20 cm.
l = 4λ →λ = ¼ = 0,25 m
t = 4λ → T = 2/4 = 0,5 s
y = ….?
Jawaban :
Y = A sin (ωtkx)
= 0,2 sin [(2π/0,5)t(2π/0,25)x]
= 0,2 sin (4πt8πx)
= 0,2 sin 4π (tx)
Soal 4
Sepotong tali yang panjangnya 5 meter, salah satu ujungnya terikat kuatsedangkan ujung yang lainnya digerakkan secara kontinu denganamplitudo 10 cm dan frekuensi 4 Hz. Jika cepat rambat gelombang padatali itu 8 m/s, tentukanlah amplitudo titik P yang terletak 1,5 meter dari ujung terikat,
Besarnya amplitudo di titik P yang berjarak 1,5 m dari ujung terikat adalah
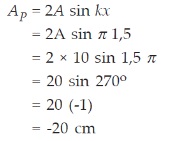
Besarnya amplitudo diambil harga mutlak/positifnya yaitu 20 cm.
Soal 5
Terdapat sepotong tali yang panjangnya 5 meter, salah satu ujungnya terikat kuat sedangkan ujung yang lainnya digerakkan secara kontinue dengan amplitudo 10 cm dan frekuensi 4 Hz. Jika cepat rambat gelombang padatali itu 8 m/s, tentukanlah amplitudo titik P yang terletak 1,5 meter dari ujung terikat !
AP = 2A sin kx
AP = 2A sin π 1,5
AP = 2 x 10 sin 1,5 π
AP = 20 sin 270°
AP = 20 (-1)
AP = -20 cm
Jadi, Besarnya amplitudo di titik P yang berjarak 1,5 m dari ujung terikat yaitu = -20 cm.
