Kesebangunan dan Kongruen : Pengertian dan Contoh Soal

√ Edu Passed Pass quality & scientific checked by advisor, read our quality control guidelance for more info
  • Review Akademik by: Review Akademik by: Sutiono M.Kom., M.T.I
  • Post author Scientific Rev by: Redaksi Haloedukasi

Apakah kalian tahu tentang kesebangunan dan kekongruenan? Pada pembahasan kali ini kita akan membahas mengenai kesebangunan dan kekongruenan. Simak pembahasannya dibawah ini.

Pengertian Kesebangunan

Kesebangunan adalah kesamaan perbandingan panjang sisi dan besar sudut antara dua bangun datar ataupun lebih.

Suatu bangun datar dikatakan kesebangunan jika memenuhi dua syarat dibawah ini :

  • Panjang sisi yang bersesuaian pada kedua bangun memiliki perbadingan nilai yang sama
  • Sudut yang bersesuaian pada kedua bangun itu sama besar

Bangun yang memiliki bentuk dan ukuran yang sama dikatakan bangun yang kongruen.

Dua bangun yang kongruen pasti sebangun, tetapi apabila dua bangun belum tentu kongruen.

Sama halnya seperti kesebangunan, kekongruenan juga memiliki syarat agar suatu bangun datar dikatakan kekongruenan :

  • Jika bangun memiliki bentuk dan ukuran yang sama
  • Sudut yang bersesuaian pada kedua bangun sama besar

Dua Bangun Datar dan Segitiga yang Sebangun

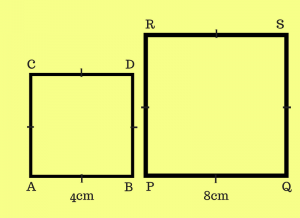
bangun datar sebangun

Kedua bangun disamping ABCD dan PQRS adalah sebangun. Kedua bangun disamping memiliki sifat :

1. Panjang sisi yang bersesuaian

pada kedua bangun memiliki perbadingan nilai yang sama. Pada gambar disamping, perbandingan panjang sisi mempunyai nilai yang sama, yaitu :

Panjang sisi AB dan PQ = AB/PQ = 4/8 = 1/2
Panjang sisi BD dan QS = BD/QS = 4/8 = 1/2
Panjang sisi DC dan SR = DC/SR = 4/8 = 1/2
Panjang sisi CA dan RP = CA/RP = 4/8 = 1/2

Jadi AB/PQ = BD/QS = DC/SR = CA/RP.

2. Sudut yang bersesuaian pada kedua bangun itu sama besar

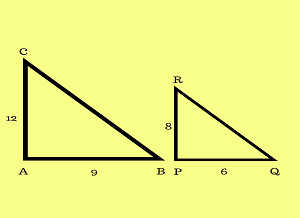
segitiga sebangun

Kedua segitiga disamping ABC dan PQR adalah sebangun. Kedua segitiga disamping memiliki sifat :

  • Panjang sisi yang bersesuaian pada kedua bangun memiliki perbandingan senilai dan hasil perbandingannya sama dengan satu. Pada gambar disamping, perbandingan sisi yang sama besar bersesuaian sama besar, yaitu:

AB bersesuaian dengan PQ = AB/PQ = 9/6 = 3/2

AC bersesuaian dengan PR = AC/PR = 12/8 = 3/2

Jadi AB/PQ = BC/QR = CA/RP

3. Sudut yang bersesuaian pada kedua bangun itu sama besar

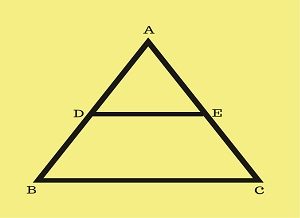
segitiga sebangun

Segitiga ABC sebangun dengan segitiga ADE, maka:

AB/AD = BC/DE = AC/AE = AD/AB = DE/BC = AE/AC

Pada segitiga siku-siku dapat dibuat garis tinggi ke sisi miring, maka diperoleh rumus :

AB2 = BD x BC ; AC2 = CD x CB ; AD2 = BD x CD

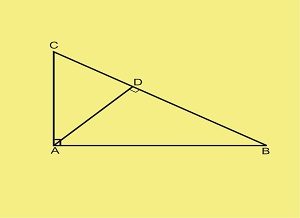
segitiga sebangun

Contoh Soal dan Pembahasan

Diketahui AC = 9cm dan AB = 12 cm. Hitung panjang BC  dan CD !

Jawab :

BC2 = AB2 + BC2
BC2 = 122 + 92
BC   = √225
BC   = 15 cm
AC2 = CD x CB
92 = CD x 15
81 = CD x l5
CD = 81/15 = 5,4 cm

Dua Bangun Datar dan Segitiga yang Kongruen
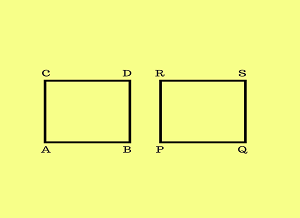
bangun datar kongruen

Kedua bangun disamping ABCD dan PQRS kongruen. Bangun datar dikatakan kongruen apabila memiliki ukuran dan bentuk yang sama.

AB = PQ
BD = QS
DC = SR
CA = RP

Sudut yang bersesuaian pada kedua bangun itu sama besar

<A = <P ; <B = <Q ; <C = <R

Pada kekongruenan segitiga, terdapat beberapa syarat diantaranya yaitu :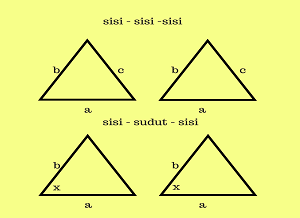
segitiga kongruen

1. Sisi – sisi – sisi

Kedua segitiga memiliki panjang sisi yang sama. Bisa dilihat pada contoh gambar disamping, segitiga tersebut kongruen.

2. Sisi – sudut – sisi

  • sisi a sama dengan sisi a
  • sudut x sama dengan sudut x
  • sisi b sama dengan sisi b

Maka segitiga di samping merupakan kongruen. Untuk penyebutannya harus sesuai dengan syarat yaitu “sisi – sudut – sisi”.
3. Sudut – sisi – sudut

  • sudut x sama dengan sudut x
  • sisi a sama dengan sisi a
  • sudut y sama dengan sudut y

Maka segitiga di samping merupakan kongruen. Untuk penyebutannya harus sesuai dengan syarat yaitu “sudut – sisi – sudut”.

fbWhatsappTwitterLinkedIn