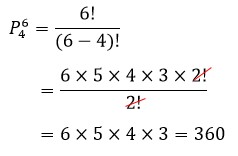Pernahkah mendengar tentang kombinatorika? Istilah ini tentunya berhubungan dengan matematika karena kombinatorika secara khusus termasuk ke dalam kelompok Matematika Diskrit.
Pembahasan kali ini akan difokuskan mengenai pengertian kombinatorika dan contoh-contoh soal yang terkait. Tak lupa pembahasan juga disertakan agar lebih memahami materi kombinatorika ini. Selamat belajar!
Apa itu Kombinatorika?
Salah satu cabang ilmu matematika tentang objek khusus adalah kombinatorika. Aspek yang berkaitan dengan kombinatorika adalah penentuan objek berdasarkan kriteria tertentu, perhitungan objek berdasarkan kriteria tertentu, penentuan objek “terbesar”, “terkecil” atau “optimal”, serta penentuan struktur suatu objek. Kombinatorika sendiri tergolong ke dalam rumpun “Diskrit” dalam matematika.
Dalam pembelajaran setingkat SMP dan SMA, kombinatorika ditemukan pada materi peluang. Jika peluang merupakan suatu cara untuk mempelajari kemungkinan terjadinya suatu peristiwa tertentu, maka kombinatorika dikhususkan pada cara penyusunan sekumpulan objek tertentu.
Contoh Soal Kombinatorika dan Pembahasan
Kombinatorika berkaitan dengan prinsip permutasi dan kombinasi. Untuk itu dalam soal-soal berikut akan selalu menggunakan prinsip kombinatorika dalam penyelesaiannya.
Soal 1
Lina diharuskan mengerjakan 8 soal dari 18 soal yang tersedia. Ketentuan dalam pengerjaan soal ini adalah soal nomor 1 sampai 5 merupakan soal yang wajib dikerjakan. Tentukan berapa banyak pilihan soal yang dapat dipilih!
Pembahasan:
Dari soal diketahui ada 18 soal, wajib mengerjakan 8 soal, sedangkan ada syarat bahwa soal no. 1-5 wajib dikerjakan, maka Lina tinggal memilih 3 soal lain selain soal no. 1-5.
Pemilihan 3 soal tersebut jika di bolak-balik urutannya akan sama saja. Misalkan Lina memilih soal nomor 10, 13, 15, maka akan sama saja ketika Lina memilih tiga soal dengan urutan 13, 10, 15. Hal ini berarti kita harus memperhatikan urutan pemilihan soal. Sehingga kita akan menggunakan prinsip kombinasi dan diperoleh,
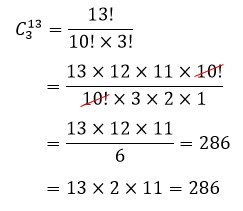
Jadi, banyak pilihan soal yang dapat dipilih oleh Lina adalah 286 macam.
Soal 2
Tangaal 24 Februari adalah ulang tahun Hani. Pada hari itu Hani merayakan ulang tahun di sebuah tempat makan, namun hanya dapat mengundang 10 dari 15 orang temannya karena keterbatasan tempat yang tersedia. Di antara 15 orang tersebut ada 5 orang sahabatnya yaitu Husein, Listy, Cepi, Dinar, dan Edwin. Hani memutuskan harus mengundang Cepi dan Listy. Dinar sudah pasti tidak bisa memenuhi undangan karena sedang keluar kota, sedangkan Edwin sedang isolasi mandiri karena terpapar Covid-19. Tentukan banyak cara yang dipunyai Hani untuk mengundang teman-temannya!
Pembahasan:
Pada soal diketahui bahwa total ada 15 orang dan ada 2 orang yang sudah terpilih yaitu Cepi dan Listy, sehingga tersisa 13 orang.
Dari 13 orang yang tersisa, ada dua orang yang tidak dapat hadir yaitu Dinar dan Edwin maka tersisa 11 pilihan teman.
Selanjutnya, kita akan mengundang 8 orang dari 11 orang yang tersisa (8 diperoleh dari 10-2, karena ada 2 orang yang sudah pasti diundang). Sehingga diperoleh,
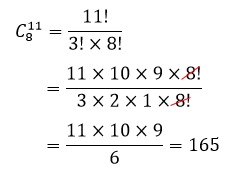
Jadi, ada 165 cara yang dipunyai Hani untuk mengundang teman-temannya.
Soal 3
Pada sebuah turnamen, sebuah tim dikatakan menang (W) jika memenangkan 2 pertandingan secara berurutan atau jika tim itu merupakan tim yang pertama kali memenangkan 4 pertandingan. Tentukan banyaknya cara turnamen tersebut dapat dilaksanakan!
Pembahasan:
Jika dimisalkan ada tim X dan tim Y dalam turnamen tersebut yang sedang bertanding, maka akan ada beberapa kemungkinan yang terjadi mengenai hasil menang(W) atau kalah(L) dari setiap tim.
| Banyak Pertandingan | Tim X | Tim Y |
| 2 3 4 5 6 7 | (W W) (L W W) (W L W W) (L W L W W) (W L W L W W) (L W L W L W W) | (L L) (W L L) (L W L L) (W L W L L) (L W L W L L) (W L W L W L L) |
Pertandingan hanya akan terjadi maksimal 7 kali. Berdasarkan tabel di atas, ada 6 x 2 = 12 cara agar turnamen bisa dilaksanakan dengan ketentuan pemenang seperti pada soal dapat terjadi.
Soal 4
Pelat kendaraan bermotor di suatu negara tersusun atas 2 angka dan 3 abjad. Pada pemilihan angka, tidak ada aturan pembatasan. Tentukan jumlah maksimum pelat yang dapat dibuat di negara tersebut!
Pembahasan:
Perhatikan bahwa pada pelat tersebut, dua elemen awal pada pelat adalah angka, maka dapat diisi angka berapapun dari 0 sampai 9. Sehingga akan diperoleh 10 x 10 = 100 susunan yang berbeda.
Tiga elemen akhir pada pelat adalah abjad. Dari abjad a sampai z ada 26 huruf, sehingga akan diperoleh 26 x 26 x 26 = 17.576 susunan yang berbeda.
Secara keseluruhan, jumlah pelat maksium yang dapat dibuat di negara tersebut adalah 100 x 17.576 = 1.757.600.
Soal 5
Sebuah bilangan terdiri dari 4 digit yang angka-angkanya disusun dari angka 1, 2, 3, 4, 5, dan 6. Tentukan banyaknya susunan bilangan yang mungkin terjadi jika angka-angkanya berlainan!
Pembahasan:
Ada dua cara untuk penyelesaian persoal ini.
- Cara pertama menggunakan metode filling slot seperti berikut,
kotak ribuan dapat diisi oleh kemungkinan dari 6 angka kotak ratusan dapat diisi oleh kemungkinan dari 5 angka kotak puluhan dapat diisi oleh kemungkinan dari 4 angka kotak satuan dapat diisi oleh kemungkinan dari 3 angka
Banyak susunan angka yang mungkin adalah 6 x 5 x 4 x 3 = 360.
- Cara kedua menggunakan prinsip permutasi.
Pada penyusunan angka, urutan angka akan membuat bilangan tersebut berbeda (perhatikan bahwa 325 ≠ 523). Karena alasan inilah kita akan menerapkan prinsip permutasi untuk penyelesaian persoalan ini.