Daftar isi
Banyak orang beranggapan bahwa matematika merupakan ilmu yang sulit, sebenarnya matematika tidak sulit itu bergantung dengan bagaimana kita menyikapinya.
Pada pembahasan kali ini akan dibahas mengenai program linear. Program linear merupakan suatu metode yang umumnya digunakan untuk memecahkan masalah pengalokasian sumber daya dengan tujuan akhir menentukan nilai minimum atau maksimum.
Pengertian Program Linear
Program linear yaitu pemecahan masalah untuk menentukan nilai minimum atau maksimum dari fungsi linear yang dibatasi oleh grafik linear dengan memperhatikan syarat-syarat yang berlaku.
Penggunaan program linear pada kehidupan sehari-hari misalkan memaksimalkan keuntungan suatu perusahaan.
Contoh lainnya yaitu meminimalkan pengeluaran suatu perusahaan.
Sistem Pertidaksamaan Linear Dua Variabel
Sistem pertidaksamaan linear dua variabel yaitu gabungan dari beberapa pertidaksamaan linear yang variabelnya saling berkaitan.
Adapun bentuk umum dari sistem pertidaksamaan linear dua variabel yaitu ax + by < c untuk tanda dapat berupa <, >, ≤, ≥. Biasanya variabel yang digunakan dalam pertidaksamaan yaitu x dan y.
Daerah Penyelesaian Sistem Pertidaksamaan Linier
Dalam menyelesaikan pada sistem pertidaksamaan linear dua variabel maka dapat diselesaikan dengan cara menentukan daerah penyelesaiannya.
Daerah penyelesaian yang akan digambar merupakan daerah himpunan yang merupakan titik (x, y) yang merupakan anggota himpunan penyelesaiannya.
Untuk lebih jelasnya langsung dengan contoh soal, simak penjelasannya dibawah ini.
Contoh :
 Diketahui sistem pertidaksamaan berikut
Diketahui sistem pertidaksamaan berikut
x + 2y ≤ 10 x ≥ 0, y ≥ 0
Jawab :
Langkah pertama buat persamaan x + 2y = 10
Buatlah dengan dua titik bantu
Misalkan x = 0, untuk x + 2y =10 maka 2y = 10 dan y = 5
Misalkan y = 0 , untuk x + 2y = 10 maka x = 10
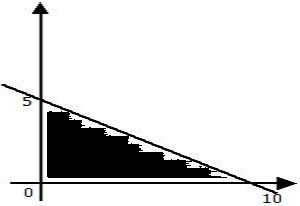
Setelah itu gambarlah daerah penyelesaian pertidaksamaannya.
Untuk mengetahui daerah penyelesaiannya uji dengan titik (0, 0)
x + 2y ≤ 10 , maka 0 + 2(0) ≤ 10
Maka berdasarkan pengujian diatas, daerah yang memuat (0, 0) merupakan daerah penyelesaian pada sistem pertidaksamaan tersebut.
Sehingga daerah penyelesaian untuk sistem pertidaksamaan linear variabel diatas digambarkan seperti gambar disamping.
Nilai Optimum
Untuk menentukan nilai optimum maka kita harus menentukan terlebih dahulu daerah penyelesaian pertidaksamaan linear, dengan begitu untuk mencari nilai optimum dapat menjadi lebih mudah.
Langkah-langkah yang harus dikerjakan ketika menentukan nilai optimum diantaranya sebagai berikut:
- Tentukan kendala dari permasalahan program linear
- Tentukan daerah penyelesaian dari pertidaksamaan yang ditanyakan
- Tentukan titik-titik pojok daru daerah penyelesaian yang telah ditemukan
- Setelah mengerjakan ketiga langkah itu, tentukan nilai optimum dari daerah penyelesaian tersebut lalu bandingkan hasil subtitusi titik-titik pojok dengan fungsi yang ditentukan dengan model matematika.
Perhatikan contoh soal cerita dibawah ini untuk lebih mempermudah
Contoh:
Toko bahagia menjual peralatan alat tulis, harga sebuah buku Rp.5.000 dan sebuah puplen Rp.2.500. Pemilik toko tersebut mempunyai modal 250.000 dan toko tersebut hanya mampu menampung hingga 50 buah. Tentukan model matematika untuk mendapatkan keuntungan jika laba dari 1 buah buku 1.000 dan dari pulpen 500?
Jawab :
1. Tentukan kendala dari permasalahan program linear tersebut
Misalkan buku = x dan pulpen = y, maka
- Fungsi Kendala
5000x + 2500y ≤ 250000 2x + y ≤ 100 x + y ≤ 50
- Fungsi Objektif
1000x + 500y
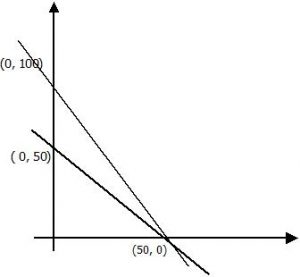
2. Tentukan daerah penyelesaian
Untuk menentukan daerah penyelesaian dapat ditentukan sama seperti pembahasan diatas
Ubah menjadi bentuk persamaan 2x + y = 100 ; x + y = 50
Buatlah dengan dua titik bantu
2x + y = 100
Misalkan x = 0, untuk 2x + y = 100 maka y = 100
Misalkan y = 0 , untuk 2x + y = 100 maka 2x = 100 dan x = 50
Maka (x, y) yaitu (0, 100) (50, 0)
x + y = 50
maka (x, y) yaitu (0, 50) (50, 0)
Setelah itu gambarlah daerah penyelesaian pertidaksamaannya.
Untuk mengetahui daerah penyelesaiannya uji dengan titik (0, 0).
3. Tentukan titik-titik pojok
Titik D dapat dicari dengan mengeliminasi dari persamaan 2x + y = 100 dan x + y = 50
2x + y = 100 x + y = 50
Maka (2x + y = 100) – (x + y) =50
ditemukan
x = 50 y = 0 D ( 50, 0)
4. Tentukan nilai optimum
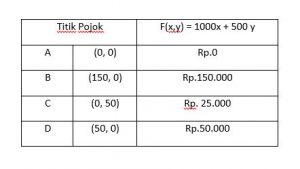
Untuk menentukan nilai optimum, maka masukkan titik pokok A, B, C, D lalu substitusikan
Titik A (0, 0 ) = 1000x + 500y maka 1000(0) + 500(0) = 0 Titik B(150, 0) = 1000x + 500y maka 1000(150) + 500(0) = 150000 Titik C (0, 50) = 1000x + 500y maka 1000(0) + 500(50) = 25000 Titik D (50, 0) = 1000x + 500y maka 1000(50) + 500(0) = 50000
Maka ditemukan nilai optimum untuk soal diatas yaitu pada titik B (150, 0 ) dengan keuntungan Rp.150.000.
Untuk memperoleh keuntungan yang maksimal maka harus menjual 150 buku dan 0 pulpen.
