Daftar isi
Materi trigonometri membahas perbandingan antar sisi segitiga, grafik fungsi trigonometri, dan sudut istimewa.
Identitas trigonometri merupakan suatu relasi atau hubungan antara suatu persamaan trigonometri dengan persamaan trigonometri lainnya.
Identitas trigonometri juga mencakup fungsi kebalikan, seperti:
- Cosecan = 1/sin
- Secan = 1/cos
- Cotangen = 1/tan
Grafik Fungsi Trigonometri
1. Grafik Sinus
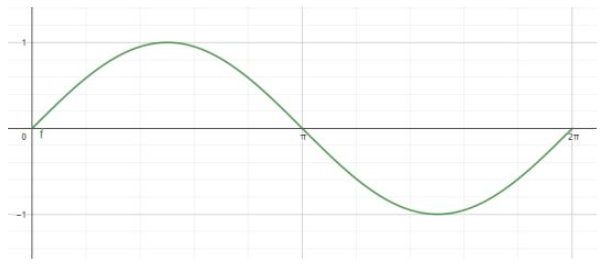
2. Grafik Cosinus
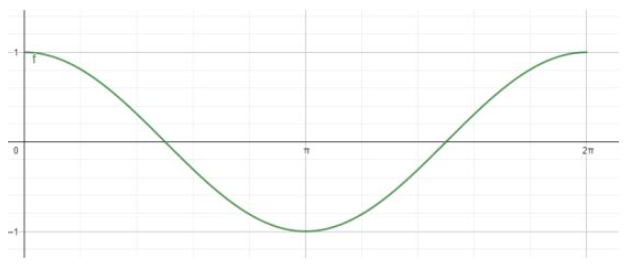
3. Grafik Tangen
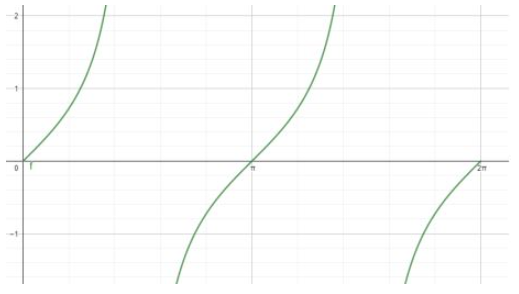
Sudut Istimewa
Sudut-sudut istimewa merupakan beberapa sudut yang dengan mudah kita tentukan nilai trigonometrinya.
Beberapa sudut istimewa tersebut yaitu 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.
Tabel Trigonometri
Perhatikan grafik fungsi sinus berikut.
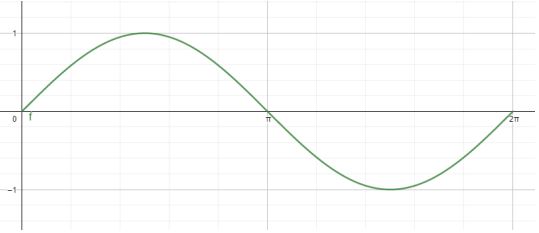
Pada grafik fungsi sinus tersebut, beberapa nilai sinusnya yaitu:
- sin 0° = 0
- sin 30° = ½
- sin 45° = ½ √2
- sin 60° = ½ √3
- sin 90° = 1
- sin 270° = -1
Perhatikan grafik fungsi cosinus berikut:
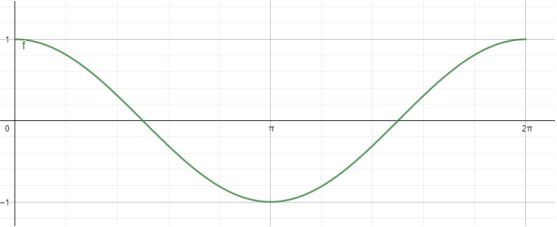
Beberapa nilai cosinus dari fungsi tersebut yaitu:
- cos 0° = 1
- cos 30° = ½ √3
- cos 45° = ½ √2
- cos 60° = ½
- cos 90° = 0
Perhatikan grafik fungsi tangen berikut:
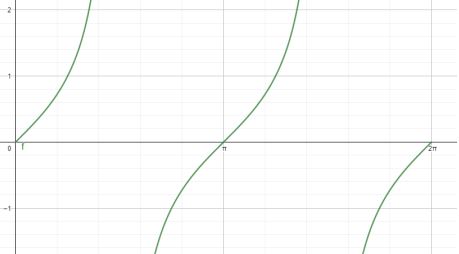
Beberapa nilai tangen dari fungsi tersebut yaitu:
- tan 0° = 0
- tan 30° = 1/√3
- tan 45° = 1
- tan 60° = √3
- tan 90° = (tidak terdefinisi)
Tabel Sin Cos Tan
Berikut merupakan tabel sinus, cosinus, dan tangen.
| α | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° |
| sin α | 0 | ½ | ½ √2 | ½ √3 | 1 | ½ √3 | ½ √2 | 1/2 | 0 |
| cos α | 1 | ½ √3 | ½ √2 | ½ | 0 | -½ | -½ √2 | -½ √3 | -1 |
| tan α | 0 | 1/√3 | 1 | √3 | -√3 | -1 | -1/√3 | 0 |
| α | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
| sin α | -1/2 | -½ √2 | -½ √3 | -1 | -½ √3 | -½ √2 | -½ | 0 |
| cos α | -½ √3 | -½ √2 | -½ | 0 | ½ | ½ √2 | ½ √3 | 1 |
| tan α | 1/√3 | 1 | √3 | -√3 | -1 | -1/√3 | 0 |
Keterangan:
α : besar sudut
Selanjutnya akan dijelaskan mengenai beberapa persamaan trigonometri.
Persamaan Trigonometri
Beberapa persamaan yang perlu kalian ketahui untuk mempermudah penyelesaian fungsi trigonometri yang lebih kompleks yaitu
- sin (90° – x) = cos x
- sin (90° + x) = cos x
- sin (180° – x) = sin x
- sin (180° + x) = – sin x
- cos (90° – x) = sin x
- cos (90° + x) = – sin x
- cos (180° – x) = – cos x
- cos (180° + x) = – cos x
Beberapa persamaan trigonometri berikut merupakan bentuk identitas trigonometri.
Identitas Trigonometri Terhadap Sinus
- sin 2x = 2 sin x cos x
- sin (a + b) = sin a cos b + cos a sin b
- sin (a – b) = sin a cos b – cos a sin b
- sin2 x = 1 – cos2x
Identitas Trigonometri Terhadap Cosinus
- cos 2x = cos2x – sin2x
- cos 2x = 2 cos2x – 1
- cos 2x = 1 – 2 sin2x
- cos2x = 1- sin2x
- cos (a + b) = cos a cos b – sin a sin b
- cos (a – b) = cos a cos b + sin a sin b
Identitas Trigonometri Lainnya
- sec2x – tan2x = 1
- sin2x + cos2x = 1
Keterangan:
x, a, b : besar sudut
Contoh Soal
1. Buktikan bahwa sec4 α – sec2 α = tan4 α + tan2 α.
Pembahasan:
sec4 α – sec2 α = tan4 α + tan2 α
sec2 α (sec2 α – 1) = tan2 α (tan2 α + 1)
sec2 α (tan2 α) = tan2 α (sec2 α)
sec2 α . tan2 α = sec2 α . tan2 α
Jadi, sec4 α – sec2 α = tan4 α + tan2 α = sec2 α . tan2 α.
Terbukti.
2. Tentukan nilai dari (sin α – cos α)2 + 2 sin α cos α.
Pembahasan:
(sin α – cos α)2 = sin2 α – 2 sin α. cos α + cos2 α
(sin α – cos α)2 = sin2 α + cos2 α – 2 sin α. cos α
(sin α – cos α)2 = 1 – 2 sin α. cos α
Selanjutnya :
(sin α – cos α)2 + 2 sin α cos α = 1 – 2 sin α. cos α + 2 sin α cos α
(sin α – cos α)2 + 2 sin α cos α = 1
Jadi, (sin α – cos α)2 + 2 sin α cos α = 1.
