Daftar isi
Dalam ilmu matematika, Bilangan Komposit merupakan kebalikan dari bilangan prima.
Lalu apa saja pengertian dan hal yang membedakannya dari bilangan prima?. Berikut pembahasannya.
Apa itu Bilangan Komposit?
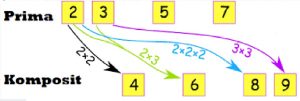
Bilangan Komposit merupakan bilangan asli yang lebih dari satu, memiliki faktor lebih dari 2, dan bukan termasuk bilangan prima.
Bilangan komposit juga bisa diartikan merupakan hasil perkalian antara dua bilangan prima atau lebih.
Beberapa orang juga yang mengartikan bahwa bilangan komposit adalah bilangan cacah selain 1 (satu) dan 0 (nol). Bilangan komposit juga biasa disebut sebagai bilangan tersusun.
Catatan:
Angka 0 dan 1 bukan termasuk bilangan komposit dan juga bukan bilangan prima.
Hal ini disebabkan karena:
Angka 0 mempunyai tak terhingga faktor dan bukan bilangan asli
Angka 1 hanya memiliki 1 faktor.
Sehingga bilangan komposit, dimulai dari angka 4.
Himpunan Bilangan Komposit
Himpunan bilangan komposit disini adalah seperti ‘kelompok’ bilangan komposit dari beberapa angka yang ditanyakan oleh soal.
- Himpunan Bilangan Komposit kurang dari 10
K = 4, 6, 8, dan 9.
(Jumlah himpunan bilangan komposit yang kurang dari 10 hanya ada 4).
- Himpunan Bilangan Komposit 1-20
K= 4, 6, 8, 9, 10, 12, 14, 15, 16, 18
(Jumlah himpunan bilangan komposit yang kurang dari 20 ada 10).
- Himpunan Bilangan Komposit antara 20-50
K= 22, 24, 25, 26, 27, 28, 30, 32, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48
(Jumlah himpunan bilangan komposit antara bilangan 20-50 ada 19).
Lambang Himpunan Bilangan Komposit
Secara umum tidak adanya lambang khusus untuk bilangan komposit, akan tetapi untuk menyatakan suatu bilangan komposit biasanya memakai simbol huruf ‘K’ (huruf k kapital) karena berasa dari kata Komposit, yang berawalan huruf K.
Cara mengetahui Bilangan Komposit
1. Angka yang memiliki lebih dari 2 faktor
Contoh:
Angka 6 termasuk bilangan komposit karena memiliki lebih dari 2 pembagi yaitu 1, 2, 3, 6.
1 karena 6 : 1 = 6
2 karena 6 : 2 = 3
3 karena 6 : 3 = 2
6 karena 6 : 1 = 6.
2. Bilangan Genap, kecuali angka 2.
Semua bilangan genap termasuk bilangan komposit karena angka genap bisa dibagi dengan banyak faktor pembagi dan tentunya menghasilkan lebih dari 2 faktor pembagi.
Angka 2 tidak termasuk bilangan komposit, angka 2 satu-satunya angka genap yang termasuk bilangan prima, karena angka 2 memiliki 2 faktor pembagi, yaitu angka 1 dan 2.
Cara menentukan Bilangan Komposit
Dalam menentukan bilangan komposit, yaitu:
Dengan menggunakan Faktor Prima dan Pohon Faktor
Faktor prima adalah bilangan-bilangan prima untuk menyusun suatu bilangan komposit.
Untuk mencari faktor prima suatu bilangan dapat menggunakan bantuan pohon faktor.
Dengan cara ini, sangat mudah menentukan bilangan komposit.
Cara mencari faktor prima suatu bilangan dengan menggunakan pohon faktor adalah dengan cara membagi angka tersebut secara terus menerus dengan bilangan prima terkecil yang memungkinkan.
Contoh:
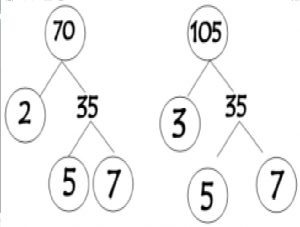
Terihat jelas bahwa angka 70 dan 105 adalah bilangan komposit, karena memiliki faktor lebih dari 2, yaitu angka 70 memiliki faktor pembagi 2, 5, 7, 35 dan angka 105 memiliki faktor pembagi 3, 5, 5, 7, 35.
Contoh Bilangan Komposit
Berikut adalah bilangan komposit dari 1-100:
| 4 | 6 | 8 | 9 | 10 | 12 | 14 | 15 | 16 | 18 | 20 | 21 | 22 | 24 | 25 | 26 | 27 | 28 | 30 | 32 | 33 | 34 | 35 |
| 36 | 38 | 39 | 40 | 44 | 45 | 46 | 48 | 49 | 50 | 51 | 52 | 54 | 55 | 56 | 57 | 58 | 60 | 62 | 63 | 64 | 65 | 66 |
| 68 | 69 | 70 | 72 | 74 | 75 | 76 | 77 | 78 | 80 | 81 | 82 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 92 | 94 | 98 | 100 |
Berikut adalah bilangan komposit dari 100-300:
| 102 | 104 | 105 | 106 | 108 | 110 | 112 | 114 | 115 | 117 | 118 | 119 | 120 | 121 |
| 122 | 123 | 124 | 125 | 126 | 128 | 129 | 130 | 132 | 133 | 134 | 135 | 136 | 138 |
| 140 | 141 | 143 | 144 | 145 | 146 | 147 | 148 | 150 | 152 | 153 | 154 | 155 | 156 |
| 158 | 159 | 160 | 161 | 162 | 164 | 165 | 166 | 168 | 169 | 170 | 171 | 172 | 174 |
| 175 | 176 | 177 | 178 | 180 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 190 | 192 |
| 194 | 195 | 196 | 198 | 200 | 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 210 |
| 212 | 213 | 214 | 215 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 | 226 |
| 228 | 230 | 231 | 232 | 235 | 236 | 237 | 240 | 242 | 241 | 243 | 244 | 247 | 248 |
| 250 | 253 | 254 | 258 | 260 | 262 | 264 | 267 | 270 | 271 | 273 | 275 | 280 | 281 |
| 282 | 283 | 285 | 289 | 290 | 292 | 293 | 295 | 296 | 297 | 298 | 299 | 300 |
Contoh Soal Bilangan Komposit
- Bilangan Komposit kurang dari 10
Jawab:
4, 6, 8, dan 9.
Berarti himpunan bilangan komposit yang kurang dari 10 ada 4 angka saja.
- Bilangan Komposit disebuah dadu
4 dan 6
Berarti, himpunan bilangan komposit yang ada di sebuah dadu hanya ada 2.
- Sepuluh bilangan komposit kurang dari 20.
4, 6, 8, 9, 10, 12, 14, 15, 16, dan 18.
Berarti himpunan bilangan komposit yang kurang dari 20 ada 10 angka saja.
- Mengapa angka 2 tidak termasuk bilangan komposit?
Angka 2 tidak termasuk bilangan komposit, walaupun angka 2 adalah angka genap, karena faktor pembagi angka 2 tidak lebih dari 2 faktor pembagi, yaitu hanya angka 1 dan dirinya sendiri.
- Bilangan 7 mengapa tidak masuk Bilangan Komposit?
Angka 7 hanya bisa dibagi oleh 1 dan 7, sehingga angka 7 hanya memiliki 2 faktor.
Untuk selanjutnya angka 7 disebut bilangan prima. Sehingga dapat diketahui setiap bilangan yang merupakan bilangan prima adalah bukan komposit.
