Daftar isi
Dalam kehidupan sehari-hari, tentunya kita sering melihat gerakan yang ada di sekeliling kita. Baik itu gerak dari makhluk hidup, maupun gerakan dari benda atau alat. Di antara gerakan benda atau alat, ada yang geraknya teratur, misalnya gerakan jarum jam, gerak roda mobil, dan lain-lain.
Gerakan tersebut terus berulang, sehingga bersifat periodik. Salah satu jenis dari gerak periodik adalah gerak harmonik sederhana.
Apa itu gerak harmonik sederhana? Simak penjelasan lengkapnya di bawah ini;
Pengertian Gerak Harmonik Sederhana
Gerak harmonik sederhana adalah gerak dari suatu benda yang berulang atau bolak balik pada sepanjang garis lintasan yang sama. Selang waktu dari bolak baliknya tetap. Getaran dari gerak bolak balik tersebut ada yang sifatnya tidak teratur, ada pula yang teratur atau harmonik.
Suatu benda dapat disebut memenuhi getaran harmonik apabila:
- Benda tersebut membentuk suatu gerak yang berulang atau bolak balik (periodik)
- Gerakan benda tersebut senantiasa melewati posisi keseimbangan
- Percepatan atau arah gaya yang bekerja pada benda selalu menuju arah keseimbangan
- Gaya atau percepatan yang bekerja pada benda tersebut sebanding dengan simpangan atau posisi benda
Contoh gerak harmonik sederhana terjadi pada getaran bandul atau pendulum. Bandul yang digantungkan pada seutas tali, saat mengayun akan bergerak di sepanjang garis atau lintasan yang sama.
Gerak harmonik juga dapat terjadi pada sistem pegas. Ketika suatu benda digantungkan pada pegas, lalu digetarkan dan pegas akan bergerak turun naik, seperti gambar berikut:

Pada gerak harmonik sederhana terdapat beberapa besaran fisika, yaitu;
- Simpangan (Y), merupakan jarak benda dari titik keseimbangannya
- Amplitudo (A), yaitu simpangan maksimum atau disebut juga jarak terjauh
- Frekuensi (f) adalah banyaknya getaran setiap waktu
- Periode (T) ialah lamanya waktu yang diperlukan dalam satu getaran
- Hubungan frekuensi dan periode dapat ditulis dalam rumus T = 1/f atau f = 1/T
Jenis Gerak Harmonik Sederhana
Gerak harmonik sederhana dibedakan menjadi dua:
- Gerak Harmonik Sederhana (GHS) Linier
Gerak harmonik sederhana linier adalah pergerakan suatu benda pada satu garis lurus. Pergerakan tersebut dapat lurus secara vertikal maupun secara horizontal.
Contoh gerak harmonik sederhana linier seperti penghisap yang ada di dalam silinder pegas, gerak osilasi air raksa atau air dalam pipa U, gerakan vertikal atau horizontal pegas, dan lain sebagainya.
- Gerak Harmonik Sederhana (GHS) Angular
Gerak harmonik sederhana angular adalah pergerakan suatu benda yang mengayun membentuk pola setengah lingkaran ataupun membentuk perputaran.
Contohnya, terjadi pada gerak suatu bandul atau bandul fisis (bandul jam), osilasi ayunan torsi, dan lain-lain.
Persamaan Gerak Harmonik Sederhana
Gerak harmonik sederhana memiliki rumus persamaan sebagai berikut:
Persamaan Kecepatan
Dalam gerak harmonik sederhana, kecepatan diperoleh dari turunan pertama persamaan simpangan, berikut ini persamaannya:

Persamaan Percepatan
Sedangkan persamaan percepatan benda yang bergerak harmonik sederhana diperoleh dari turunan pertama persamaan kecepatan atau merupakan turunan kedua persamaan simpangan. Persamaan percepatan gerak harmoni sederhana adalah sebagai berikut:
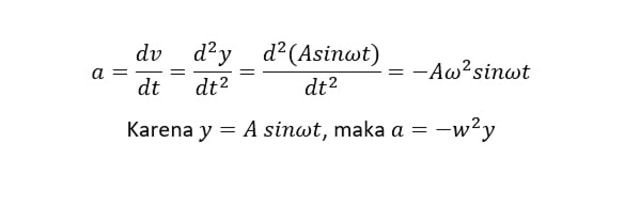
Simpangan maksimum mempunyai nilai yang sama dengan amplitudo (y = A), sehingga percepatan maksimumnya adalah am= – Aw
Persamaan Energi
Persamaan energi pada gerak harmonik sederhana meliputi energi kinetik, energi potensial, dan energi mekanik. Berikut ini rumus persamaannya:
Energi Kinetik
Rumus persamaan energi kinetik benda sebagai berikut:
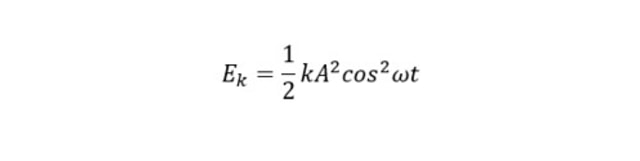
Energi Potensial
Untuk persamaan energi potensial benda dapat dirumuskan seperti berikut:
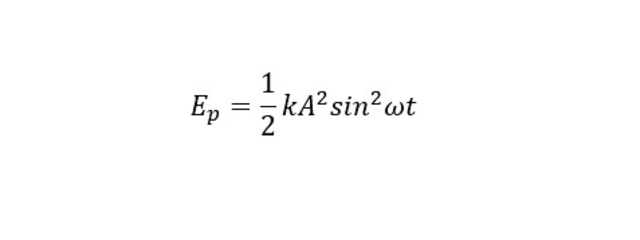
Energi Mekanik
Energi mekanik adalah penjumlahan dari energi kinetik dan energi potensial. Maka rumus persamaannya seperti di bawah ini:
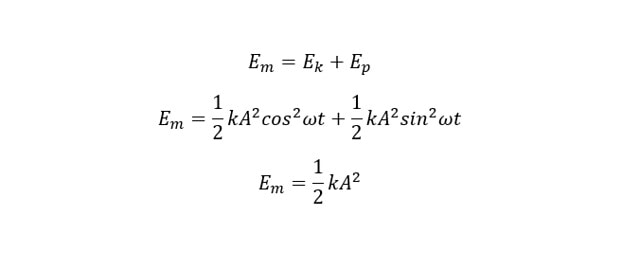
Keterangan:
k = nilai ketetapan (N/m)
ω = kecepatan sudut (rad/s)
A = amplitudo (m)
t = waktu tempuh (s)
Catatan:
Jumlah energi potensial dan energi kinetik benda yang bergerak harmonik sederhana akan selalu bernilai tetap.
Persamaan Simpangan pada GHS
Pada gerak harmonik sederhana, simpangan dianggap sebagai proyeksi dari partikel yang bergerak secara beraturan pada diameter lingkaran. Maka rumus simpangan pada GHS adalah sebagai berikut:
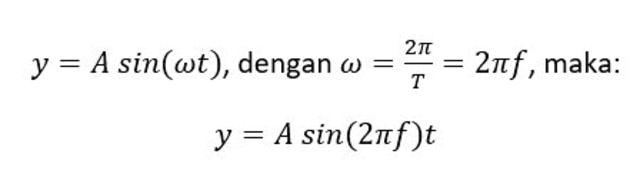
Keterangan:
y = simpangan getaran (m)
ω = kecepatan sudut (rad/s)
T = periode (s)
f = frekuensi (Hz)
t = waktu tempuh (s)
A = amplitudo/simpangan maksimum (m)y = simpangan getaran (m)
Sistem Pegas – Massa
Di bawah ini merupakan gambar dari skema gerak harmonis sederhana sistem beban-pegas:
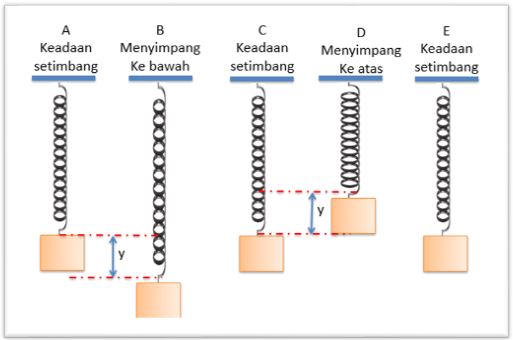
Gerakan yang terjadi pada pegas dari A-E adalah gerakan satu kali dari getaran pegas. Rumus periode sistem massa pegas (T) sebagai berikut:
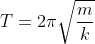
Sedangkan rumus frekuensi getar sistem massa pegas (f) adalah:
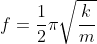
Keterangan:
m = massa beban
k = konstanta pegas
Getaran pada Sistem Bandul Matematis
Sebelum lebih lanjut lagi pada penjelasan sistem bandul matematis, perhatikan gambar bandul berikut:

Berdasarkan gambar di atas dapat dijelaskan bahwa, satu kali getaran bandul adalah gerakan dari B-A-B-C-B. Maka rumus persamaan periode getar bandul (T) adalah:
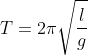
Sedangkan rumus persamaan sistem massa pegas (f) sebagai berikut:
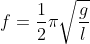
Keterangan:
g = percepatan gravitasi
I = panjang tali bandul
Contoh Soal Gerak Harmonik Sederhana
Supaya lebih jelas tentang gerak harmonik sederhana, perhatikan contoh soal berikut ini:
Apabila ada sebuah pegas yang memiliki konstanta pegas sebesar 500 N/m. Lalu suatu benda dengan massa 0,2 kg digantungkan pada pegas tersebut dan ditarik ke bawah sejauh 5 cm dari posisi kesetimbangan, lalu dilepaskan. Tentukan frekuensi, periode, amplitudo, simpangan, dan percepatan maksimum getaran benda tersebut!
Pembahasan:
Diketahui:
Konstanta pegas (k) = 500 N/m
Massa benda (m) = 0,2 kg
Simpangan awal (y) = 5 cm = 0,05 m
Maka frekuensi (f) gerakannya adalah:
Periode (T) gerakannya:
Amplitudo:
Amplitudo (A) gerakan sama dengan simpangan maksimum pada gerakan tersebut, sehingga diketahui:
Simpangan:
Simpangan (s) pada titik waktu tertentu dapat dihitung seperti berikut:
Pada t = 0, simpangan adalah 0 sebab benda dilepaskan dari posisi kesetimbangan.
Pada t = T/4, simpangan mencapai nilai maksimum positif, sehingga:
Percepatan:
Percepatan maksimum gerakan sebagai berikut:
Jadi:
Frekuensi getaran: 7,97 Hz
Periode getaran: 0,1255 s
Amplitudo gerakan: 0,05 m
Simpangan pada titik waktu tertentu: 0,003 m
Percepatan maksimum gerakan: -125 m/s^2
