Daftar isi
Sebelumnya telah dibahas mengenai bangun datar berupa persegi, lingkaran, dll.
Di dalam rumus matematika, objek-objek bangun datar ini dapat dicariposisi titik koordinatnya.
Caranya adalah dengan menggunakan koordinat kartesius.
Apa itu koordinat kartesius dan bagaimana cara menghitungnya akandijelaskan pada pembahasan berikut ini.
Pengertian Koordinat Kartesius
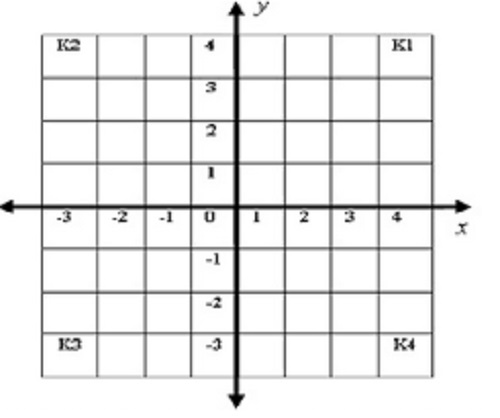
Koordinat kartesius merupakan alat bantu untuk menentukan posisi titik pada suatu objek bangun datar.
Titik ini digambarkan dalam bentuk 2 bilangan yakni koordinat absis (x) dan koordinat ordinat (y).
Untuk dapat menentukan titik koordinat ini, maka yang dibutuhkan adalah 2 sumbu melintang vertikal yakni sumbu (y) dan horizontal yakni sumbu (x).
Fungsi Koordinat Kartesius
Fungsi dari adanya koordinat kartesius adalah untuk menentukan suatuobjek tersebut berada pada posisi titik mana saja dimana menggunakan bilangankoordinat (x) dan (y).
Manfaat Koordinat Kartesius
Manfaat adanya koordinat kartesius antara lain:
- Digunakan dalam bidang penerbangan untukmenentukan objek pesawat agar tidak menabrak objek lainnya.
- Digunakan dalam peta untuk menentukan titiklokasi suatu tempat.
- Memudahkan pengiriman paket melalui peta yangsudah terlihat jelas koordinatnya.
- Digunakan dalam bidang pelayaran untukmenentukan posisi kapal di atas permukaan laut.
- Untuk mencari suatu objek yang hilang di bawahpermukaan laut.
Sistem Koordinat
Sistem pada koordinat kartesius ada 2 yaitu:
- Sistem Koordinat 2 Dimensi

Sistem koordinat ini terdiri dari 2 sumbu yang tegak lurus melintang dengan arah horizontal (x) dan vertikal (y).
Titik pertemuannya adalah angka 0 atau pusat koordinat (0, 0).
Karena 2 sumbu ini saling melintang ke kanan kiri dan atas bawah, sehingga membuatnya terbagi menjadi 4 bagian yang disebut kuadran.
| Kuadran | Nilai (x) | Nilai (y) | Keterangan |
| Kuadran I | > 0 | > 0 | Kedua koordinat (x, y) memiliki nilai positif |
| Kuadran II | < 0 | > 0 | Koordinat (x) memiliki nilai negatif, (y) positif |
| Kuadran III | > 0 | < 0 | Koordinat (x) memiliki nilai positif, (y) negatif |
| Kuadran IV | < 0 | < 0 | Kedua koordinat (x, y) memiliki nilai negatif |
- Sistem Koordinat 3 Dimensi
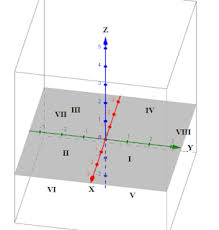
Sistem koordinat ini terdiri dari 3 sumbu yang saling melintang diantaranya sumbu (x), sumbu (y) dan sumbu (z).
Karena melintangnya 3 sumbu ini, menjadikannya terpisah 8 bagian yang disebut oktan.
| Oktan | Nilai (x) | Nilai (y) | Nilai (z) | Keterangan |
| Oktan I | > 0 | > 0 | > 0 | Koordinat (x, y, z) memiliki nilai positif |
| Oktan II | > 0 | < 0 | > 0 | Koordinat (x) positif (y) negatif (z) positif |
| Oktan III | < 0 | < 0 | > 0 | Koordinat (x) negatif (y) negatif (z) positif |
| Oktan IV | < 0 | > 0 | > 0 | Koordinat (x) negatif (y) positif (z) positif |
| Oktan V | > 0 | > 0 | < 0 | Koordinat (x) positif (y) positif (z) negatif |
| Oktan VI | > 0 | < 0 | < 0 | Koordinat (x) positif (y) negatif (z) negatif |
| Oktan VII | < 0 | < 0 | < 0 | Koordinat (x, y, z) memiliki nilai negatif |
| Oktan VIII | < 0 | > 0 | < 0 | Koordinat (x) negatif (y) positif (z) negatif |
Diagram Kartesius
Diagram kartesius merupakan penentuan titik pada gambaran objek dalam sistem koordinat yang terdiri dari sumbu x dan y.
Sehingga dalam hal ini, tiap-tiap titik pada objek ditentukan oleh koordinat (x) dan (y).
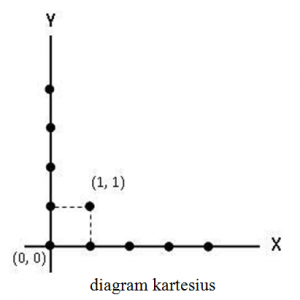
Keterangan:
- Titik koordinat bertuliskan angka (1, 1).
- Cara membaca titik koordinat dimulai dari koordinat (x) lalu (y).
- Garis potongan sumbu (x) dan (y) diberi angka 0.
- Bagian atas sumbu (x) dan bagian kanan sumbu (y) memiliki nilai positif.
- Bagian bawah sumbu (x) dan bagian kiri sumbu (y) memiliki nilai negatif.
Cara menentukan Koordinat Kartesius
Koordinat berisi bilangan berupa titik (x) dan titik (y) dan cara penulisannya adalah (x, y).
Cara menentukannya adalah sebagai berikut:
- Angka pertama yang ditulis adalah titik yang terletak pada koodinat(x)
- Tarik garis lurus dari atas titik ke sumbu (x), maka itulah angka (x).
- Angka kedua yang ditulis adalah titik yang terletak pada koordinat (y)
- Tarik garis lurus dari titik menuju ke sumbu (y), maka itulah angka (y).
Contoh Soal dan Pembahasan Koordinat Kartesius
1. Berapa tiap-tiap koordinat yang membentuk bangun trapesium pada diagram kartesius di bawah ini? Sebutkan!
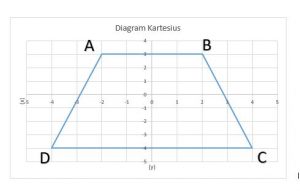
Jawab:
Bila ditarik garis lurus pada masing-masing sudut trapesium, maka sebagai berikut:
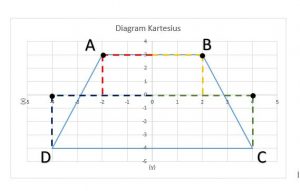
Dibaca pertama kali (x) lalu (y) = (x, y), sehingga jawabannya adalah:
- Koordinat A = (-2, 3)
- Koordinat B = (2, 3)
- Koordinat C = (4, -4)
- Koordinat D = (-4, -4)
2. Desi, Dito, Ana dan Pedro merupakan teman dari kecil. Apabila melihat sebuah peta, rumah mereka berbentuk persegi panjang.
Jika rumah Desi berada di koordinat (5, 2), rumah Ana di koordinat ( 11, 2) dan rumah Pedro ada di koordinat ( 5, 8).
Maka di koordinat mana rumah Dito?
Diketahui:
Fakta persegi panjang adalah sisi atas sama dengan sisi bawah dan sisi kanan sama dengan sisi kiri.
- Rumah Desi (A) = (5, 2)
- Rumah Pedro (B) = (5, 8)
- Rumah Ana (C) = (11, 2)
Ditanyakan Rumah Dito (D)…?
Jawab:
Sehingga apabila digambar menjadi diagram kartesius, maka:
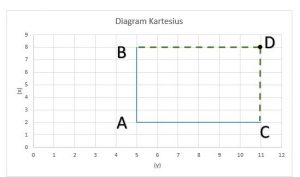
Jadi jawabannya adalah rumah Dito ada pada koordinat (11, 8)
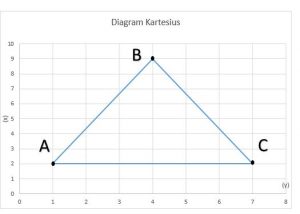
3. Perhatikan gambar diagram kartesius di bawah ini!
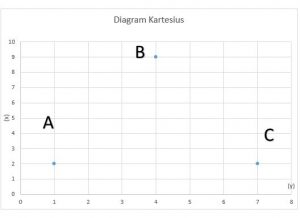
a. Tentukan masing-masing koordinat A, B, dan C!
b. Objek bangun datar apakah yang terbentuk?
c. Hitung keliling objek bangun datar tersebut!
Jawab:
a. Bila ditarik lurus menuju sumbu x dan y, maka gambar diagram tersebut menjadi:
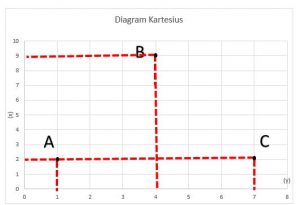
- Koordinat A = (1, 2)
- Koordinat B = (4 9)
- Koordinat C = (7, 2)
b. Bila ditarik membentuk objek maka hasilnya adalah bangun datar segitiga seperti pada gambar berikut:
c. Diketahui:
- Rumus Keliling segitiga = 3s = a + b + c
- a = koordinat (y) B – koordinat (y) A = 9 – 2 = 7
- b = koordinat (y) B – koordrinat (y) C = 9 – 2 = 7
- c = koordinat (x) C – koordinat (x) A = 7 – 1 = 6
Ditanyakan keliling segitiga…?
Jawaban:
Keliling segitiga = a + b + c
= 7 + 7 = 6
= 20
Jadi keliling segitiga pada diagram kartesius di atas adalah 20.
