Daftar isi
Kali ini kita akan membahas mengenai polinomial, berikut pembahasannya.
Apa itu Polinomial?
Dalam dunia matematika, polinomial atau suku banyak adalah pernyataan matematis yang berhubungan dengan jumlahan perkalian pangkat dalam satu atau lebih variabel dengan koefisien.
Bentuk umum dari suatu polinomial adalah sebagai berikut:
anxn+…+a2x2+a1x1+a0
dimana a merupakan koefisien konstan, dan pangkat tertinggi pada polinomial tersebut menandakan orde atau derajatnya, sehingga polinomial diatas memiliki derajat atau orde n.
Pembagian Polinomial
Pada umumnya, bentuk umum dari pembagian polinomial adalah:
F(x) = P(x) × H(x) + S(x)
Dimana
- F(x) : suku banyak
- H(x) : hasil bagi
- P(x) : pembagi
- S(x) : sisa
Sebelum kita memahami metode pembagian polinomial, terlebih dahulu kita harus mengetahui tentang teorema sisa yaitu
Misalkan F(x) merupakan polinomial berderajat n,
Jika F(x) dibagi (x-k) maka hasilnya adalah F(k)
Jika F(x) dibagi (ax-b) maka hasilnya adalah F(b/a)
Jika F(x) dibagi (x-a)(x-b) maka hasilnya adalah
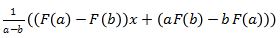
Untuk metode pembagian polinomial terdapat beberapa cara, diantaranya:
Metode Pembagian Biasa
Contohnya adalah jika 2x3 – 3x2 + x + 5 dibagi dengan 2x2 – x – 1
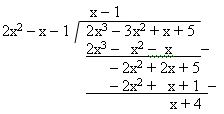
maka hasil bagi dan sisanya adalah hasil bagi = x-1 dan sisa = x+4
Metode Horner
Metode ini dipakai untuk pembagi yang berderajat 1 ataupun pembagi berderajat n yang bisa difaktorkan jadi pembagi-pembagi dengan derajat 1.
Langkah langkah:
1) Tulis koefisien dari polinomialnya → harus urut dari koefisien xn, xn – 1, … hingga konstanta (untuk variabel yang tidak memiliki koefisien, maka ditulis 0). Misalkan untuk 5x3 – 8, koefisien-koefisiennya adalah 5, 0, 0, dan -8.
2) Untuk koefisien dengan derajat tertinggi P(x) ≠ 1, hasil baginya harus dibagi dengan koefisien derajat tertinggi P(x)
3) Jika pembagi dapat difaktorkan menjadi
- P1 dan P2, maka S(x) = P1 × S2 + S1
- P1, P2, P3, maka S(x) = P1×P2×S3 + P1×S2 + S1
- P1, P2, P3, P4, maka S(x) = P1×P2×P3×S4 + P1×P2×S3 + P1×S2 + S1
- dan seterusnya.
Metode Koefisien Tak Tentu
Pada dasarnya, metode ini dikerjakan dengan cara mensubstitusikan F(x) berderajat m dan P(x) berderajat n ke dalam bentuk umum pembagian polinomial, kemudian H(x) dan S(x) nya diisi dengan
H(x) merupakan polinomial berderajat k, dimana k = m – n
S(x) merupakan polinomial berderajat n-k.
Contoh Soal Polinomial
1. Polinomial f(x) ÷ (x – 2) sisanya 24 serta f(x) ÷ (x + 5) sisanya 10. Maka f(x) tersebut dibagi x2 + 3x – 10 sisanya yaitu…
Jawab:
Rumusnya yaitu:
P(x) = H(x) . Pembagi + (px + q)
Diketahui:
- f(x) ÷ (x – 2) sisa 24, maka:
f(x) = H(x)(x – 2) + 24
Kemudian subtitusikan x = 2, sehingga:
f(2) = H(2)(2 – 2) + (2p + q)
= 2p + q = 24 …. (i)
f(x) ÷(x + 5) sisa 10, sehingga:
f(x) = H(x)(x + 5) + 10
Dengan Subtitusikan x = -5, sehingga:
(f(-5) = H(-5)(-5 + 5) + (-p + q)
= -5p + q = 10 …. (ii)
Eliminasikan persamaan (i) serta (ii):
2p +q =24
-5p +q =10
7p = 14
p =2
Dalam mensubtitusikan p = 2 pada 2p + q = 24
2(2) + q = 24
q = 24 – 4
q = 20
Apabila f(x) dibagi x2 + 3x – 10 maka:
f(x) = H(x) (x2 + 3x – 10) + (px + q)
f(x) = H(x) (x-2) (x + 5) + (px + q)
Sisa px + q = 2x + 20
2. Suku banyak x4 – 3x3 – 5x2 + x – 6 dibagi oleh x² – x -2 sisanya sama dengan …
Jawab:
Diketahui pembaginya yaitu: x² – x -2, sehingga:
x² – x -2= 0
(x – 2) (x + 1) = 0
x = 2 dan x = -1
Ingat rumus: P(x) = H(x) + (px + q), sehingga sisanya (px + q), maka:
- x = 2
f(2) = 2p + q
24 – 3(2)3 – 5(2)2 + 2 – 6 = 2p + q
16 – 24 – 20 + 2 – 6 = 2p + q
-32 = 2p + q … (i)
- x = -1
f(-1) = -p + q
(-1) – 3(-1)3 – 5(-1)2 + (-1) – 6 = -p + q
1 + 4 – 5 – 1 – 6 = -p + q
-8 = -p + q …(ii)
Eliminasikan persamaan (i) serta (ii), menjadi:
-32 =2p +q
-8 =-p +q
-24 =3p
p = -8
Jika kita substitusikan p = –p + q = -8
-(-8) + q = -8
q = -16
Maka , sisanya adalah = p + q = -8x – 16
3. Misalkan diketahui:
F(x) = 2x3 – 3x2 + x + 5
P(x) = 2x2 – x – 1
Tentukan hasil bagi dan sisanya
Jawab:
F(x) = 2x3 – 3x2 + x + 5
P(x) = 2x2 – x – 1 = (2x + 1)(x – 1)
Sehingga p1 : (2x + 1) = 0 -> x = -1/2 dan p2 : (x – 1) = 0 -> x = 1
Kemudian langkah hornernya ditunjukkan pada gambar berikut:
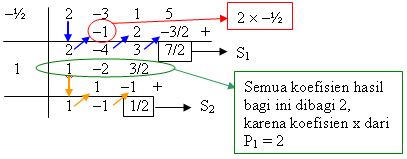
Jadi, diperoleh hasil dan sisanya sebagai berikut:
H(x) = x-1
S(x) = P1×S2 + S1 = x + 4
4. Misalkan diketahui
F(x) = 2x3 – 3x2 + x + 5
P(x) = 2x2 – x – 1
Tentukan hasil bagi dan sisanya menggunakan metode koefisien tak tentu!! Pembahasan
m = 3, n = 2, k = 1
H(x) berderajat 1 misalkan H(x) = ax+b
S(x) berderajat 2-1=1 misalkan S(x) = px+q
Substitusikan F(x), P(x), H(x), S(x) ke persamaan
F(x) = P(x) . H(x) + S(x), maka diperoleh
2x3 – 3x2 + x + 5 = (2x2 – x – 1)(ax+b) + px+q
2x3 – 3x2 + x + 5 = 2ax3 + 2bx2 – ax2 – bx – ax – b + px + q
(2)x3 + (– 3)x2 + (1)x + (5) = (2a)x3 + (2b– a)x2 + (– b – a + p) x + (– b + q)
5. F(x) = 2x3 – 3x2 + x + 5 dibagi dengan P(x) = 2x2 – x – 1
H(x) berderajat 3 – 2 = 1
S(x) berderajat 2 – 1 = 1
Sehingga, misalnya H(x) = ax + b dan S(x) = cx + d
Maka:
2x3 – 3x2 + x + 5 = (2x2 – x – 1).(ax + b) + (cx + d)
Ruas kanan menjadi:
= 2ax3 + 2bx2 – ax2 – bx – ax – b + cx + d
= 2ax3 + (2b – a)x2 + (–b – a + c)x + (–b + d)
Samakan koefisien ruas kiri dan juga ruas kanan, sehingga menjadi:
x3 → 2 = 2a → a = 2/2 = 1
x2 → –3 = 2b – a → 2b = –3 + a = –3 + 1 = –2 → b = –2/2 = –1
x → 1 = –b – a + c → c = 1 + b + a = 1 – 1 + 1 → c = 1
Konstanta → 5 = –b + d → d = 5 + b = 5 – 1 → d = 4
Sehingga hasil akhirnya adalah:
Sehingga hasil akhirnya adalah:
H(x) = ax + b = 1.x – 1 = x – 1 S(x) = cx + d = 1.x + 4 = x + 4.
