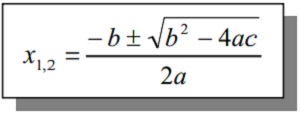
Rumus abc merupakan salah satu cara menentukan akar-akar dari suatu persamaan kuadrat yang paling sering digunakan dalam matematika.
Ada tiga cara yang biasa digunakan ilmu matematika matematika dalam dalam menyelesaikan akar persamaan kuardat, yaitu dengan memfaktorkan, melengkapkan akar kuadrat, dan menggunakan salah satu rumus penyelasaian permsamaan kuadrat sebagaimana disinggung di atas.
Ada beberapa istilah yang harus dipahami terlebih dahulu sebelum kita berlanjut membahas mengenai rumus abc. Adapun istilah-istilah yang sangat berkaitan tersebut adalah sebagai berikut:
1. Polinom
Dalam bahasa kita polinom sering disebut dengan suku banyak, yaitu suatu suku yang tersusun dengan banyak terhingga yang terdiri atas unsur berupa variabel dan konstanta.
2. Fungsi Kuadrat
Fungsi sendiri diartikan sebagai bentuk hubungan (relasi) dalam suatu himpunan tertentu yang disebut sebagai domain (daerah asal) dengan nilai tunggal yang biasa dimisalkan dengan f (x) yang berasal dari himpunan lain, biasa disebut dengan kodomain.
Sedangkan yang dimaksud dengan fungsi kuadrat adalah bentuk dari fungsi dimana pangkat terbesar dari variabel yang terdapat didalamnya adalah 2 (dua).
Dalam suatu fungsi pasti adalah polinom. Bentuk umum dari fungsi kuadrat adalah y =ax2+ bx + c.
3. Persamaan kuadrat
Persamaan suatu bentuk permisalan dalam matematika yang bertujuan untuk menyatakan bahwa dua hal adalah sama persis.
Sedangkan yang dimaksud dengan persamaan kuadrat adalah bentuk persamaan polinom yang pangkat dari variabelnya paling besar adalah 2 (dua). Bentuk umum dari persamaan kuadrat adalah ax2+ bx + c = 0.
Setelah memahami istilah-istilah penting di atas, barulah kemudian kita bisa memahami lebih lanjut mengenai apa dan bagaimana menggunakan rumus abc dalam menyelesaikan persamaan kuadrat. Adapun caranya adalah sebagai berikut:
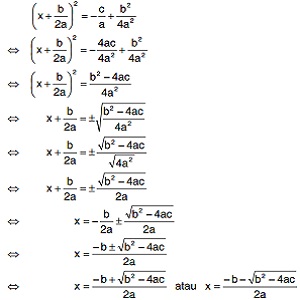
Rumus Kuadrat
Rumus ini sering juga disebut sebagai rumus kuadrat. Teknik dari mendapatkan turunan dari rumus kuadrat ini adalah dengan melengkapkan kuadrat sempurna terlebih dahulu, sebagai berikut:
Bentuk umum akar kuadrat adalah:
ax2 + bx + c = 0
Kedua ruas dari bentuk tersebut ditambah dengan “ -c” sehingga berubah menjadi:
ax2 + bx = -c
Kemudian kedua ruas dibagi dengan “ a” sehingga menjadi:
x2 + b/a.x = - c/a
Terakhir adalah melengkapi kuadrat pada ruas kiri, dengan cara ditambah (b/2a)2 pada kedua ruas maka akan diperoleh bentuk sebagai berikut:
x2 + b/a x+ (b/2a)2 = c/a + (b/2a)2
Kemudian nyatakan dalam bentuk kuadrat sempurna dengan cara sebagaimana gambar disamping.
Sehingga nantinya akan didapati suatu bentuk rumus yang dalam persamaan kuadrat disebut rumus abc.
Metode rumus ini merupakan metode paling umum yang sering digunakan dalam menyelesaikan akar-akar persamaan kuadrat yang bentuk umumnya adalah ax2+ bx + c = 0.
Jadi bagi anda penggemar matematika jangan sampai lupa bentuk rumus yang permisalan umumnya.
Permisalan tersebut adalah cara paling mudah dalam menyelesaikan akar persamaan kuadrat.
Perlu diketahui bahwa untuk membentuk turunan dari rumus kuadrat kita harus memahami terlebih dahulu cara melengkapkan akar kuadrat, sebab dalam prosesnya hal itu diperlukan.
Contoh:
Dengan menggunakan rumus kuadrat tentukanlah akar-akar persamaan kuadrat dari x2 + 6x + 5 = 0?
Jawab:
Pertama ingat terlebih dahulu bahwa persamaan kuadrat merupakan bentuk polinom yang tentunya memiliki variabel dan koefisien.
Setelah memahami apa saja koefisien dari bentuk persamaan kuadrat dan mengetahui nilainya kemudian subtitusikan kedalam bentuk rumus di atas.
Koefisien dari persamaan kuadrat x2 + 6x + 5 = 0 adalah a = 1, b = 6, c = 5. Sehingga jika koefisien tersebut kemudian di subtitusikan kedalam rumus adalah sebagaimana gambar disamping.
Sifat-sifat Persamaan Kuadrat
1. Jumlah dan hasil kali akar-akar persamaan kuadrat
Jika x1 dan x2 adalah akar-akar persamaan kuadrat ax2 + bx + c = 0 dengan a ≠ , jumlah dan hasil kali akar-akar persamaan kuadrat itu ditentukan dengan rumus;
2. Diskriminan persamaan kuadrat
Dengan cara melihat diskriminan dari persamaan kuadrat ax2 + bx + c = 0 dengan a ≠ 0 dan D = b2–4ac.
Dapat diketahui jenis-jenis akar persamaan kuadrat sebagai berikut:
Jika D > 0, kedua akarnya bilangan real (nyata) yang berbeda
Jika D = 0, kedua akarnya bilangan real (nyata) dan sama
Jika D < 0, kedua akarnya bilangan kompleks.
