Jajar genjang merupakan salah satu bangun datar yang memiliki dua pasang rusuk yang sejajar dengan ukuran panjang yang sama dengan pasangannya.
Dalam bahasa Inggris bangun datar ini biasa disebut dengan nama parallelogram.
Bangun datar ini memiliki dua pasang sudut yang besarnya tiap sudut sama dengan sudut di depannya.
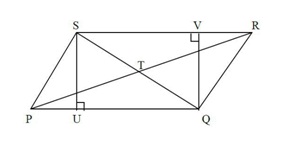
Untuk lebih jelasnya berikut adalah gambar dari jajaran genjang dan sifat-sifat khusus yang dimilikinya:
- Setiap sisi yang berhadapan selalu berukuran sama dan sejajar. Misalnya sisi PQ sejajar dengan SR , sementara sisi QR sejajar dengan SP.
- Setiap sudut yang berhadapan berukuran sama. Misalnya sudut Q sama dengan sudut S, dan sudut P sama dengan sudut R.
- Dua sudut besar yang berdekatan berukuran 180 derajat.
- Tidak memiliki simetri lipat tetapi mempunyai simetri putar tingkat dua.
- Mempunyai masing – masing dua sudut lancip dan sudut tumpul.
- Semua sudutnya jika dijumlahkan adalah 360 derajat.
Untuk menghitung luas jajaran genjang kita menggunakan rumus yang sama seperti yang kita gunakan untuk menghitung luas persegi panjang.
Yang menbedakan adalah pada jajaran genjang ukuran panjang di ganti menjadi alas (a), sementara untuk lebarnya diganti menjadi tinggi (t). sehingga apabila ditulis rumusnya menjadi seperti berikut:
L = a x t
Keterangan :
L = luas jajar genjang
a = alas
t = tinggi
Begitu pula jika kita ingin menghitung keliling dari jajaran genjang, maka caranya pun sama dengan menghitung keliling dari persegi panjang.
K = PQ + QR + RS + SP
Keterangan:
K = keliling jajar genjang
PQ + QR + RS + SP = panjang masing-masing sisi jajaran genjang
Jika panjang PQ = RS dan panjang QR = SP, maka rumus keliling jajar genjang dapat di rumuskan sebagai berikut:
K = 2 x ( PQ + QR )
atau
K = 2 x alas + 2 x sisi miring
Pada dasarnya jajaran genjang dan persegi panjang memiliki prinsip yang sama.
Jika bagian kiri jajaran genjang dipotong dan kemudian digabungkan dengan bagian di sebelah kanan, maka terbentuklah sebuah persegi panjang.
Karena dua bangun datar ini memiliki prinsip yang sama maka untuk menghitung luas dan kelilingnya pun kita menggunakan prinsip yang sama.
