Aturan Sinus dan Cosinus: Pengertian dan Contoh Soalnya

√ Edu Passed Pass quality & scientific checked by advisor, read our quality control guidelance for more info
  • Review Akademik by: Review Akademik by: Sutiono M.Kom., M.T.I
  • Post author Scientific Rev by: Redaksi Haloedukasi

Dalam materi ini, dibahas mengenai aturan sinus dan cosinus disertai contoh soal agar mempermudah dalam pemahaman.

Aturan Sinus

Apa itu Aturan Sinus?

Aturan sinus menyatakan bahwa perbandingan panjang sisi sebuah segitiga dengan sinus sudut yang menghadapnya memiliki nilai yang sama.

Perhatikan gambar segitiga berikut:

aturan sinus

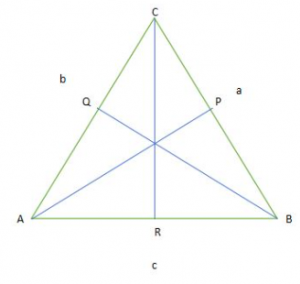
Keterangan:

  • A = besar sudut di hadapan sisi a
  • a = panjang sisi a
  • B = besar sudut di hadapan sisi b
  • b = panjang sisi b
  • C = besar sudut di hadapan sisi c
  • c = panjang sisi c
  • AP ┴ BC
  • BQ ┴ AC
  • CR ┴ AB

Perhatikan segitiga ACR

Sin A = CR/b  maka CR = b sin A …(i)

Perhatikan segitiga BCR

Sin B = CR/a  maka CR = a sin B …. (ii)

Perhatikan segitiga ABP

Sin B = AP/c maka AP = c sin B … (iii)

Perhatikan segitiga APC

Sin C = AP/b  maka AP = b sin C …(iv)

Berdasarkan persamaan (i) dan (ii) diperoleh

CR = b sin A = a sin B maka a/sin A = b/sin B …(v)

Berdasarkan persamaan (3) dan (4) didapat

AP = c sin B = b sin C maka b/sin B = c/sin C …(vi)

Kemudian, berdasarkan persamaan (v) dan (vi) diperoleh

a/sin A = b/sin B = c/sin C

Persamaan ini yang kemudian disebut dengan aturan sinus.

Contoh Soal Aturan Sinus

1. Diketahui segitiga ABC dengan besar sudut A adalah 60o, sudut B adalah 45o, dan panjang sisi AC sama dengan 10 cm. Panjang BC pada segitiga ABC tersebut adalah ….

Pembahasan:

Perhatikan gambar segitiga ABC dengan ukuran sesuai yang diketahui pada soal berikut ini.

Soal Aturan Sinus

Untuk mencari panjang BC dapat menggunakan rumus aturan sinus.

Panjang BC adalah:

\[ \frac{AC}{Sin \; B} = \frac{BC}{Sin \; A} \]
\[ \frac{10}{Sin \; 45} = \frac{BC}{Sin \; 60} \]
\[ \frac{10}{\frac{1}{2} \sqrt{2}} = \frac{BC}{\frac{1}{2} \sqrt{3}} \]
\[ \frac{1}{2} \sqrt{2} \times BC = 10 \times \frac{1}{2} \sqrt{3} \]
\[ BC = \frac{ 10 \times \frac{1}{2} \sqrt{3}}{\frac{1}{2} \sqrt{2}} \]
\[ BC = \frac{ 10 \sqrt{3}}{\sqrt{2}} \; \textrm{cm} \]

Dari hasil di atas diperoleh panjang BC, namun untuk mendapatkan nilai yang paling sederhana perlu langkan mengalikan dengan akar rasional, seperti terlihat pada langkah berikut.

\[ BC = \frac{ 10 \sqrt{3}}{\sqrt{2}} \times \frac{ \sqrt{2} }{\sqrt{2}} \]
\[ BC = \frac{ 10 \sqrt{6}}{2} = 5 \sqrt{6} \; \textrm{cm} \]

2. Diketahui sebuah segitiga ABC memiliki luas sebesar 6cm2. Jika panjang AB = 3cm dan BC = 4cm, tentukan besar ∠ABC!

Pembahasan:

L = ½ × AB × BC × Sin ∠AB
6cm2 = ½ × 3cm × 4cm × Sin ∠AB
6cm2 = 6cm2 × Sin ∠AB
Sin ∠ABC = 
ABC = arc sin (1
ABC = 90o

Jadi, besar ∠ABC adalah 90o.

b2 = a2+ c2 – 2ac cos 
c2 = a2+ b2 – 2ab cos C

Aturan Cosinus

Apa itu Aturan Cosinus?

Aturan cosinus menjelaskan hubungan antara kuadrat panjang sisi dengan nilai cosinus dari salah satu sudut pada segitiga.

Perhatikan segitiga berikut:

aturan cosinus

Keterangan:

  • A = besar sudut di hadapan sisi a
  • a = panjang sisi a
  • B = besar sudut di hadapan sisi b
  • b = panjang sisi b
  • C = besar sudut di hadapan sisi c
  • c = panjang sisi c
  • AP ┴ BC
  • BQ ┴ AC
  • CR ┴ AB

Perhatikan segitiga BCR

Sin B = CR/a maka CR = a sin B
Cos B = BR/a maka BR = a cos B
AR = AB – BR = c – a cos B

Perhatikan segitiga ACR

b2  = AR2 + CR2
b2  = (c – a cos B)2 + (a sin B)2
b2  = c2 – 2ac cos B + a2 cos2 B + a2 sin2 B
b2  = c2 – 2ac cos B + a2 (cos2 B + sin2 B)
b2  = c2 + a2– 2ac cos B

Menggunakan analogi yang sama, kemudian diperoleh aturan cosinus untuk segitiga ABC sebagai berikut:

a2 = c2 + b2– 2bc cos A

Contoh Soal Aturan Cosinus

1. Diberikan segi empat ABCD seperti pada gambar di bawah!

Contoh soal aturan sinus dan aturan cosinus

Panjang BC adalah ….

Pembahasan:

Mencari panjang AC dengan aturan sinus:

\[ \frac{AC}{Sin \; D} = \frac{AD}{Sin \; C} \]
\[ \frac{AC}{Sin \; 30^{o}} = \frac{10}{Sin \; 45^{o}} \]
\[ \frac{AC}{\frac{1}{2}} = \frac{10}{\frac{1}{2} \sqrt{2}} \]
\[ AC = \frac{10 \times \frac{1}{2}}{\frac{1}{2} \sqrt{2}} \]
\[ AC = \frac{10}{\sqrt{2}} \]
\[ AC = \frac{10}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} \]
\[ AC = \frac{10 \sqrt{2}}{2} = 5 \sqrt{2} \]

Mencari panjang BC dengan aturan cosinus:

\[ BC^{2} = AC^{2} + AB^{2} - 2 \cdot AC \cdot AB \cdot Sin \; A \]
\[ BC^{2} = (5 \sqrt{2})^{2} + (10 \sqrt{2})^{2} - 2 \cdot (5 \sqrt{2}) \cdot (10 \sqrt{2}) \cdot Cos \; 60^{o} \]
\[ BC^{2} = 50 + 200 - 200 \cdot \frac{1}{2} \]
\[ BC^{2} = 250 - 100 \]
\[ BC^{2} = 150 \]
\[ BC = \sqrt{150} \]
\[ BC = \sqrt{25 \times 6} \]
\[ BC = 5 \sqrt{6} \; \textrm{cm} \]

2. Diketahui sebuah segitiga ABC memiliki sisi dengan panjang

a = 10 cm

c = 12 cm

besar sudut B = 60̊.

Hitung panjang sisi b!

Pembahasan:

b2 = a2+ c2 – 2ac cos B
b2 = 100+144 – 44 cos 60̊
b2 = 244 – 44(0,5)
b2 = 244 – 22
b2 = 222
b = 14,8997

Jadi, panjang sisi b adalah 14,8997 cm.

fbWhatsappTwitterLinkedIn

Related Posts