Daftar isi
Pada pembahasan kali ini kita akan membahas mengenai efek compton.
Pengertian Efek Compton
Efek Compton adalah istilah yang digunakan untuk hasil yang tidak biasa diamati ketika sinar-X yang tersebar pada beberapa bahan. Menurut teori klasik, ketika gelombang elektromagnetik dihamburkan dari atom, panjang gelombang radiasi yang dihamburkan diharapkan sama dengan panjang gelombang radiasi datang.
Berlawanan dengan prediksi fisika klasik ini, pengamatan menunjukkan bahwa ketika sinar-X dihamburkan dari beberapa bahan, seperti grafit, sinar-X yang dihamburkan memiliki panjang gelombang yang berbeda dari panjang gelombang sinar-X yang datang.
Fenomena klasik yang tidak dapat dijelaskan ini dipelajari secara eksperimental oleh Arthur H. Compton dan rekan-rekannya, Compton memberikan penjelasannya pada tahun 1923.
Untuk menjelaskan pergeseran panjang gelombang yang diukur dalam percobaan, Compton menggunakan gagasan Einstein tentang cahaya sebagai partikel. Efek Compton memiliki tempat yang sangat penting dalam sejarah fisika karena menunjukkan bahwa radiasi elektromagnetik tidak dapat dijelaskan sebagai fenomena gelombang murni.
Penjelasan tentang efek Compton memberikan argumen yang meyakinkan kepada komunitas fisika bahwa gelombang elektromagnetik memang dapat berperilaku seperti aliran foton, yang menempatkan konsep foton di tanah yang kokoh.
Hamburan Efek Compton
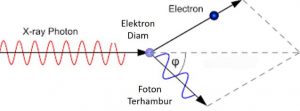
Data eksperimen menunjukkan efek Compton untuk hamburan sinar-X dari grafit pada berbagai sudut: Intensitas berkas hamburan memiliki dua puncak.
Satu puncak muncul pada panjang gelombang radiasi insiden dan puncak kedua muncul pada panjang gelombang
Pemisahan
antara puncak tergantung pada sudut hamburan
yang merupakan posisi sudut detektor di (Gambar) .
Data eksperimen pada gambar ini diplot dalam satuan arbitrer sehingga ketinggian profil mencerminkan intensitas pancaran sinar di atas kebisingan latar belakang.
Hamburan Compton adalah contoh hamburan tidak elastis , di mana radiasi yang tersebar memiliki panjang gelombang yang lebih panjang daripada panjang gelombang radiasi datang. Dalam penggunaan hari ini, istilah “hamburan Compton” digunakan untuk hamburan inelastis foton oleh partikel bermuatan bebas.
Dalam hamburan Compton, memperlakukan foton sebagai partikel dengan momentum yang dapat ditransfer ke partikel bermuatan memberikan latar belakang teoretis untuk menjelaskan pergeseran panjang gelombang yang diukur dalam eksperimen; ini adalah bukti bahwa radiasi terdiri dari foton.
Rumus Efek Compton
Persamaan Einstein
E = mc2
E = m c c = p c
Dimana
- E = Energi (J)
- m= massa (kg)
- c = kecepatan cahaya (m/s).
Rumus Energi Foton Planck
E = hf
p = hf
p = h/λ
dimana
- p = momentum foton (Ns)
- h = tetapan Planck (Js)
- f = frekuensi gelombang elektromagnetik (Hz)
- c = laju cahaya (m/s)
- λ = panjang gelombang foton (m).
Contoh Soal Efek Compton
Contoh 1 :
Sebuah kristal tunggal garam dapur (NaCl) disinari dengan berkas sinar-X dengan panjang gelombang 0,250 nm, dan pemantulan Bragg pertama diamati pada sudut 26,3°C. Berapa jarak antar atom untuk NaCl?
Jawab :
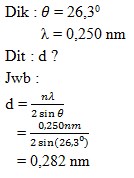
Contoh 2 :
Sebuah keping logam yang energi ambangnya sebesar 4 ev disinari dengan cahaya monokromatis dengan panjang gelombang 8000 Å hingga elektron meninggalkan permukaan logam. Jika h = 6,6 × 10−34 Js dan kecepatan cahaya 3 × 108 m/detik, maka energi kinetik elektron yang lepas….
Diketahui:
W0 = 4 eV = 4 1,6 x 10−19 = 6.4 10−19J
λ = 8000 Å = 8 10-7
Penyelesaian:
E = Wo + Ek
h c/ λ = Wo + Ek
6,6 × 10−34 3 108 / 8 10-7 = 6.4 10−19 + Ek
2.475 10-19 = 6.410−19 + Ek
Ek = 3.925 10−19 J
Jadi energi kinetic electron tersebut sebesar 3.925 10−19 J
Contoh 3 :
Elektron yang mula-mula diam dipercepat pada beda potensial 10000 volt. Tentukan :
- Panjang gelombang de Broglie
- Momentum elektron!
Diketahui:
V = 20000 volt
Penyelesaian:
p = h/λ
mv = h/λ
λ = h/mv
kita merujuk pada persamaan
QV = ½ mv2
v = √ (2QV/m)
substitusikan persamaan tersebut
λ = h/sqrt(2QV/m)
λ = 6.6 10-24/ √ (2 1.6 10-19 9.1 10-31 2 104)
λ = 6.6 10-24/ 7.63 10-24
λ = 0.864 pm
Jadi panjang gelombang de Broglie adalah 0.864 pm
p = hf
p = 6.6 10-34/8.64 10-11
p = 0.76 10-23
Jadi besar momentum elektrom tersebut adalah 0.76 10-23.
Contoh 4 :
Hitung peruhahan panjang gelombang foton yang dihamburkan dengan sudut hambur 530 , jika diketahui massa elektron 9,1 x 10-31 Kg !
Jawab:
Untuk menjawab soal ini kita bisa gunakan rumus efek Compton seperti yang tertulis di bahwah ini
λ′−λ=hmoc(1−cosφ) karena yang ditanyakan adalah perubahan panjang gelombang foton yang dihamburkan rumus di atas bisa kita rubah menjadi seperti yang tertulis di bawah ini.
Δλ=hmoc(1−cosφ)
Kemudian bisa kita subtitusikan
h = konstanta Planck 6,6 x 10-34 Js
c = laju cahaya 3 x 108 m/s
mo = massa elektron 9,1 x 10-31 Kg
Δλ=6,6×10−349,1×10−31×3×108(1−cos53)
Δλ=6,6×10−119,1×3(1−35)
Δλ=2,2×10−119,1(25)
Δλ=9,67×10−13 meter
Besar perubahan panjang gelombanng foton yang dihamburkan adalah Δλ=0,967 pm
Contoh 5 :
Sinar x yang mula-mula memiliki energi 200 KeV mengalami hamburan Compton dan dibelokan dengan sudut 600 . Besar energi sinar x yang terhambur adalah ?
Jawab:
Langkah pertama kita tinjau terlebih dahulu rumus hamburan Compton di bawah ini
λ′−λ=hmoc(1−cosφ)
Kita subtitusikan besar sudut hamburan yang terjadi dalam soal diatas
λ′−λ=hmoc(1−cos600)
λ′−λ=hmoc(12)
Kemudian kita tinjau persamaan energi foton seperti berikut
E=hf
E=hcλ
λ=hcE
Persaman panjang gelombang di atas bisa kita subtitusikan ke dalam persamaan hamburan Compon sebagai berikut
λ′−hcE=hmoc(12)
Kita bisa dapatkan persamaan panjang gelombang hamburan foton sebagai berikut
λ′=h2moc+hcE
Pada soal ini yang ditanyakan adalah besar enenrgi yang terhambur, persamaannya bisa kita tuliskan sebagai berikut
E′=hcλ′
Kita subtitusikan persamaan panjang gelombang foton yang terhambur pada persamaan di atas
E′=hch(12moc+cE)
E′=cc(12moc2+1E)
E′=1(E+2moc2E2moc2)
Persamaan besar energi foton yang terhambur setelah menumbuk elektron adalah
E′=E2moc2E+2moc2
Untuk mempermudah perhitungan lebih baik kita hitung dulu nilai moc2
moc2=9,1×10−31(3×108)2
moc2=8,19×10−14 Joule
Kemudian bisa kita hitung lengkap nilai energi foton yang terhambur setelah menumbuk elektron
E′=2×2×105×1,6×10−19×8,19×10−142×105×1,6×10−19+2×8,19×10−14
E′=2,68×10−14 Joule
E′=167313,6 eV
Besar energi yang terhambur adalah
E′=167,3136 KeV.
Contoh 6 :
Hitung panjang gelombang de Broglie dari elektron yang memiliki laju sepertiga kecepatan cahaya !
Jawab:
Untuk menjawab soal ini bisa kita gunakan rumus panjang gelombang di Broglie seperti tertulis di bawah ini
λ=hmv
λ=6,6×10−349,1×10−31×108
λ=6,69,1×10−11
λ=0,725×10−11
λ=7,25×10−12 meter
Panjang gelombang de Broglie elektron yang memiliki kecepatan sepertiga kecepatan cahaya adalah
λ=7,25 pm
Contoh 7 :
Hitung panjang gelombang de Broglie dari elektron yang memiliki laju sepertiga kecepatan cahaya !
Jawab:
Untuk menjawab soal ini bisa kita gunakan rumus panjang gelombang di Broglie seperti tertulis di bawah ini
λ=hmv
λ=6,6×10−349,1×10−31×108
λ=6,69,1×10−11
λ=0,725×10−11
λ=7,25×10−12 meter
Panjang gelombang de Broglie elektron yang memiliki kecepatan sepertiga kecepatan cahaya adalah
λ=7,25 pm
Kesimpulan Pembahasan
Foton muncul dengan energi lebih sedikit setelah tumbukan. Akibatnya, frekuensi gelombang foton yang muncul berubah. Hal inilah yang dinamakan efek compton.
