Daftar isi
Pengertian Limit Trigonometri
Trigonometri merupakan cabang dari ilmu matematika yang mempelajari hubungan antara panjang dan sudut segitiga, biasanya digunakan dalam membuat desain bangunan, pembuatan jembatan, dan pada bidang astronomi.
Sedangkan limit trigonometri merupakan nilai paling dekat dari suatu sudut. Istilah-istilah yang ada dalam trigonometri yaitu sinus (sin), cosinus (cos), tangen (tan), secan (sec), cosecan (csc), dan cotangent (ctg).
ada saat menentukan nilai dari suatu limitnya, beberapa cara/metode yang sering dipakai adalah substitusi, pemfaktoran, turunan, dan kali sekawan.
Dalam trigonometri, terdapat beberapa rumus yang berbentuk seperti di bawah ini:
1. Rumus kebalikan
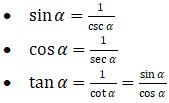
2. Rumus identitas
- sin2α + cos2α = 1
- 1 + cot2α = csc2α
- 1 + tan2α = sec2α
3. Rumus jumlah dan selisih trigonometri
- sin (α + β) = sin α cos β + cos α sin β
- sin (α – β) = sin α cos β – cos α sin β
- cos (α + β) = cos α cos β – sin α sin β
- cos (α – β) = cos α cos β + sin α sin β
4. Rumus perkalian
- 2 cos α cos β = cos (α + β) + cos (α – β)
- 2 cos α sin β = sin (α + β) – sin (α – β)
- 2 sin α cos β = sin (α + β) + sin (α – β)
- – 2 sin α sin β = cos (α + β) – cos (α – β)
5. Sudut rangkap
- sin 2α = 2 sin α cos α
- cos 2α = 1 – 2 sin2α = cos2α – sin2α
- tan 2α =
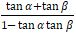
- cot 2α =
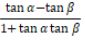
Turunan Trigonometri
| f (x) | f’(x) |
| sin x | cos x |
| cos x | – sin x |
| tan x | sec2 x |
| cot x | – csc2 x |
| sec x | sec xtanx |
| csc x | – csc xcot x |
Keenam jenis rumus di atas merupakan hal yang mendasar dari materi trigonometri, karena hampir setiap soal yang menyangkut geometri pasti menggunakan rumus-rumus tersebut.
Limit Fungsi Trigonometri
Sama halnya dengan limit trigonometri, limit fungsi trigonometri merupakan nilai paling dekat dari suatu sudut pada fungsi trigonometri.
Dalam penghitungannya, terdapat 2 (dua) teorema yang menjadi dasar dari limit fungsi trigonometri seperti di bawah ini:
Teorema 1 (hanya berlaku pada saat x → 0)
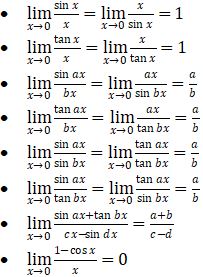
Teorema 2 (hanya berlaku pada saat x → c, Ɐc ∈ R)
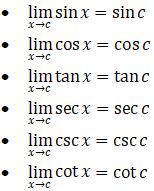
Menggunakan 2 (dua) teorema di atas, kita dapat mencari nilai dari sebuah limit trigonometri dengan lebih mudah.
Dalam sebuah soal limit fungsi trigonometri pula, biasanya menggunakan sudut-sudut istimewa yang nilainya tidak rumit.
Sudut-sudut istimewa dalam trigonometri yaitu 0o, 30o, 45o, 60o, 90o. Agar lebih mudah dalam memahami sudut istimewa, perhatikan tabel sudut istimewa dari 4 kuadran di bawah ini:
Kuadran 1
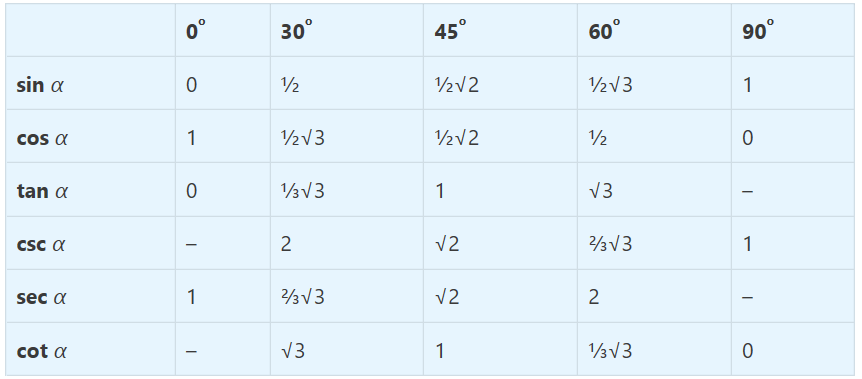
Kuadran 2
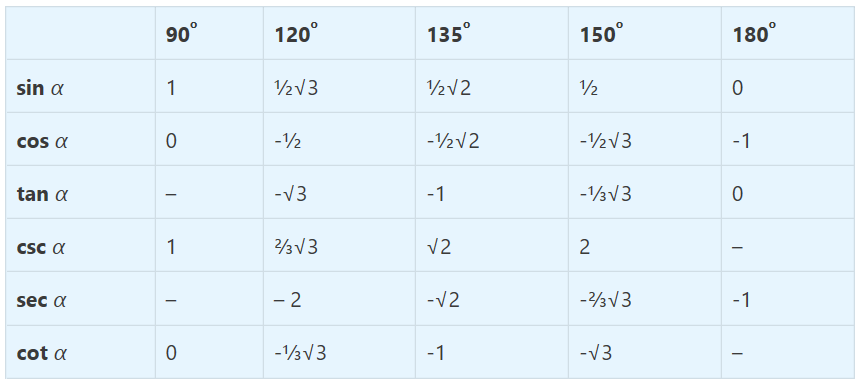
Kuadran 3
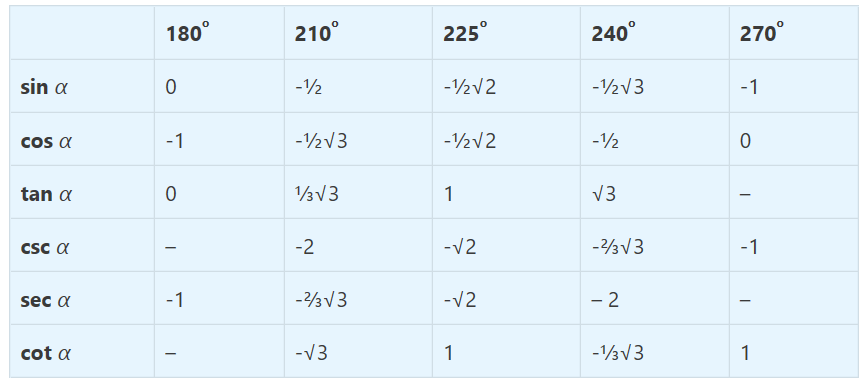
Kuadran 4
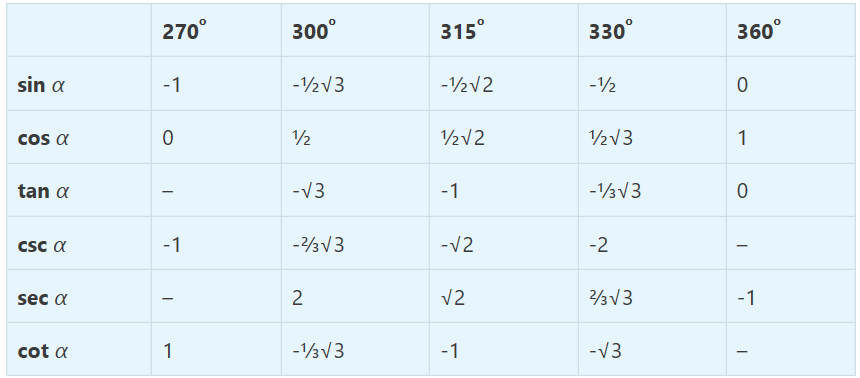
Contoh Soal Limit Trigonometri

4. Diberikan sebuah bentuk limit trigonometri sebagai berikut
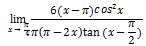
Tentukan hasil operasi limit di atas!Pembahasan
Untuk mengerjakan soal ini, kamu harus melihat kembali identitas trigonometri dan teorema limit trigonometri.
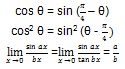
Dari indentitas trigonometri dan teorema limit trigonometri di atas, kita dapat menyelesaikan soal limit trigonometrinya.
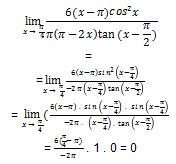
Jadi, hasilnya adalah
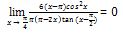
5. Terdapat sebuah fungsi campuran seperti di bawah ini
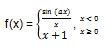
Berapakah nilai a jika limit di x = 0?Pembahasan
Pertama, untuk mengerjakan soal ini, kita harus memberlakukan batas limit kanan dan kiri.
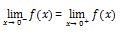
- Uji nilai pada ruas kiri
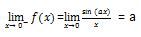
- Uji nilai pada ruas kanan
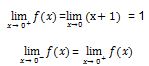
a = 1
Untuk memenuhi persamaan di atas, maka nilai a=1.
