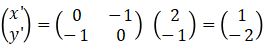Daftar isi
Pada materi ini dijelaskan definisi transformasi geometri disertai rumus, dan terdapat contoh soal disertai pembahasan untuk mempermudah pemahaman.
Apa itu Transformasi Geometri?
Transformasi geometri merupakan perubahan posisi dari posisi awal ke posisi yang lainnya.
Dalam perubahan posisi tersebut terdapat aturan tertentu yang menyebabkan posisi suatu objek berubah.
Jenis Transformasi Geometri
Dalam materi ini akan dibahas empat macam transformasi geometri. Macam-macam transformasi geometri yang akan dibahas yaitu translasi (pergeseran), refleksi (pencerminan), rotasi (perputaran), dan dilatasi (perkalian).
Translasi (Pergeseran)
Translasi merupakan perubahan posisi tanpa mengubah bentuk dan ukuran. Jadi yang berpindah hanya posisi awalnya saja, sedangkan ukuran dan bentuknya tetap.
Misalkan terdapat suatu objek dengan posisi awal (x, y) dan dilakukan translasi (a, b). Maka posisi akhir objek setelah translasi yaitu:
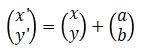
Refleksi (Pencerminan)
Konsep pencerminan ini sama dengan ketika kita bercermin. Jaran antara benda dengan cermin akan sama dengan jarak bayangan dengan cermin. Dalam koordinat kartesius terdapat beberapa jenis pencerminan sebagai berikut:
- Pencerminan terhadap titik O(0,0)
Pencerminan suatu titik yang dicermikan terhadap titik O(0, 0) memiliki matriks transformasi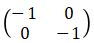 
. Sehingga rumus bayangan hasil refleksi suatu titik (x, y) terhadap titik O(0, 0) yaitu:
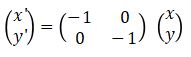
- Pencerminan terhadap sumbu x
Pencerminan suatu titik yang dicerminkan terhadap sumbu-x memiliki matriks transformasi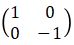 
. Sehingga bayangan terhadap suatu titik (x, y) dengan pencerminan terhadap sumbu-x yaitu:
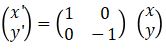
- Pencerminan terhadap sumbu-y
Pencerminan terhadap sumbu-y memiliki matriks transformasi 
. Sehingga hasil refleksi (pencerminan) suatu titik (x, y) dengan sumbu refleksi adalah sumbu-y adalah
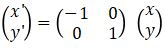
- Pencerminan terhadap garis y = x
Matriks transformasi untuk refleksi suatu titik terhadap garis y = x yaitu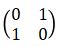 
. Sehingga bayangan hasil refleksi (pencerminan) dari titik (x, y) terhadap garis y = x adalah
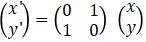
- Pencerminan terhadap garis y = -x
Adapun matriks transformasi dari refleksi terhadap garis y = -x adalah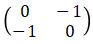 
. Sehingga untuk menentukan bayangan (hasil refleksi) terhadap garis y = -x dapat diperoleh dengan
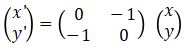
Rotasi (Perputaran)
Pada transformasi geometri berupa perputaran, unsur yang harus ada dalam rotasi adalah pusat rotasi dan besar sudut rotasi.
Secara umum, untuk suatu titik (x, y) jika dirotasi dengan pusat rotasi (p, q) dan sudut rotasi α, maka hasil rotasi (bayangan) dapat ditentukan dengan rumus berikut
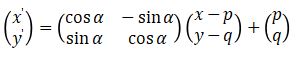
Dilatasi (Perkalian)
Pada dilatasi, objek mengalami perpindahan dan perubahan ukuran. Perubahan ukuran didasarkan pada nilai faktor dilatasi. Misalkan faktor dilatasi disimbolkan dengan k, maka:
- Jika k > 1 maka bangun akan diperbesar dan terletak terhadap pusat dilatasi dengan bangun semula.
- Jika k = 1 maka bangun tidak mengalami perubahan ukuran dan letak.
- Jika 0 < k < 1 maka bangun akan diperkeci dan terletak searah terhadap pusat dilatasi dengan bangun semula.
- Jika -1 < k < 0 maka bangun akan diperkecil dan terletak berlawanan arah terhadap pusat dilatasi dengan bangun semula.
- Jika k = -1 maka benda tidak berubah ukuran tetapi arah benda berlawanan dengan arah semual.
- Sedangkan jika k < -1 maka bangun akan diperbesar dan terletak berlawanan dengan arah bangun semula.
Secara umum, suatu objek yang terletak pada (x, y) yang didilatasi dengan faktor dilatasi k dan pusat dilatasi (p, q) adalah
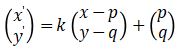
Contoh Soal Transformasi Geometri
1. Suatu titik (3, 4) ditranslasikan dengan translasi (2, -1). Tentukan bayangan hasil translasi tersebut.
Pembahasan
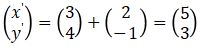
2. Pada bidang kartesius, terdapat suatu titik yang terletak pada koordinat (2, -1). Tentukan hasil pencerminannya jika titik tersebut dicerminakn terhadap titik O (0,0), terhadap sumbu – x, terhadap sumbu-y, terhadap garis y = x, dan terhadap garis y = -x.
Pembahasan
- Pencerminan terhadap titik O(0, 0)
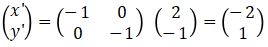
- Pencerminan terhadap sumbu-x
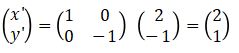
- Pencerminan terhadap garis sumbu-y
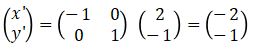
- Pencerminan terhadap garis y = x
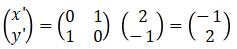
- Pencerminan terhadap garis y = -x
