Daftar isi
Istilah bunga tabungan atau bunga bank tentu sudah tidak asing bagi kita. Bunga tabungan atau bunga bank hasil tabungan seorang nasabah biasanya dihitung menggunakan penghitungan bunga tunggal serta bunga majemuk. Di sekolah, pembelajaran tentang suku bunga dipelajari di kelas ekonomi dan akuntansi.
Dalam artikel ini, akan dibahas tentang bunga majemuk. Berikut ini penjelasan lengkapnya:
Pengertian Bunga Majemuk
Bunga majemuk atau yang dalam istilah asingnya disebut Intrayear Compounding adalah pemberian bunga dari pihak bank dalam jangka atau kurun waktu tertentu kepada nasabah. Bunga majemuk dapat diberikan oleh bank terhadap nasabah lebih dari satu kali dalam setahun, sesuai dengan periode yang ditentukan untuk pemberian bunga majemuk tersebut.
Bunga majemuk menghitung penambahan bunga berdasarkan pada jumlah tabungan setiap memasuki periode baru. Hal ini membuat bunga majemuk bisa memberikan pendapatan lebih besar kepada nasabah, dibandingkan dengan penghasilan dari bunga tunggal. Oleh karena itu bunga majemuk akan mengalami perubahan di setiap periodenya.
Rumus Bunga Majemuk
Berikut ini merupakan rumus bunga majemuk, dimana untuk setiap tabungan awal M0 dengan tingkat bunga majemuk p% per tahun. Maka penghitungannya menggunakan rumus bunga majemuk sebagai berikut:
Mn = M0 (1+p)n
Dimana:
Mn : tabungan setelah n tahun;
M0 : tabungan awal;
p : persentase bunga;
n : banyaknya tahun.
Contoh Bunga Majemuk
Berikut ini 10 contoh soal bunga majemuk:
1. Contoh Soal 1
Jika tabungan awal di bank Rp4.000.000 dengan bunga majemuk 2,4% per tahun. Berapakah total tabungan setelah 8 bulan?
Pembahasan:
Pertama, tentukan dahulu persentase bunga setiap bulan.
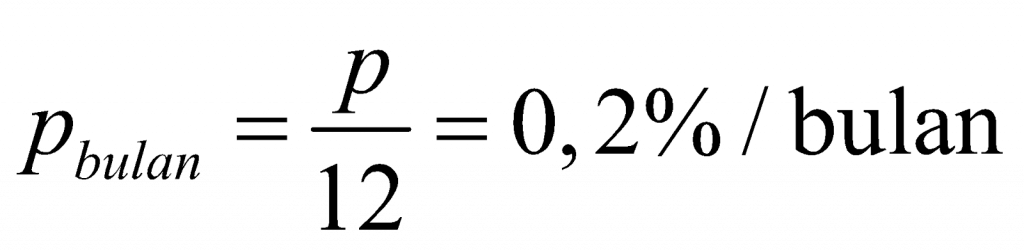
Selanjutnya, substitusikan pbulan itu pada rumus bunga majemuk, dengan n ganti n bulan.
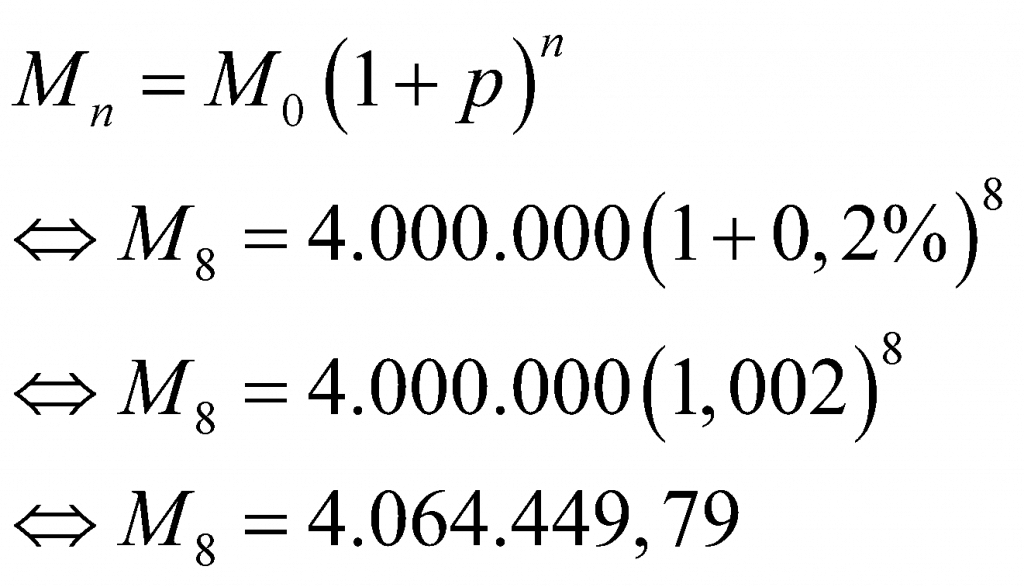
Jadi, jumlah tabungan setelah 8 bulan adalah Rp4.064.449,79.
2. Contoh Soal 2
Untuk mendata angka kelahiran, Pemerintah Daerah kota Maju Jaya mengadakan kunjungan door to door selama kurun waktu 10 tahun. Berdasarkan pendataan tersebut, dapat diketahui bahwa angka kelahiran per tahun di kota tersebut mencapai 8% dari total penduduk. Jika jumlah penduduk tahun 2010 adalah 45.000, berapa perbandingan jumlah penduduk tahun 2010 dan 2020?
Pembahasan:
Diketahui:
n = 10 tahun (2011 – 2020)
p = 8%
M0 = 45.000
Ditanya: M0 : M10 =…?
Jawab:
Pertama, tentukan jumlah penduduk tahun 2020.
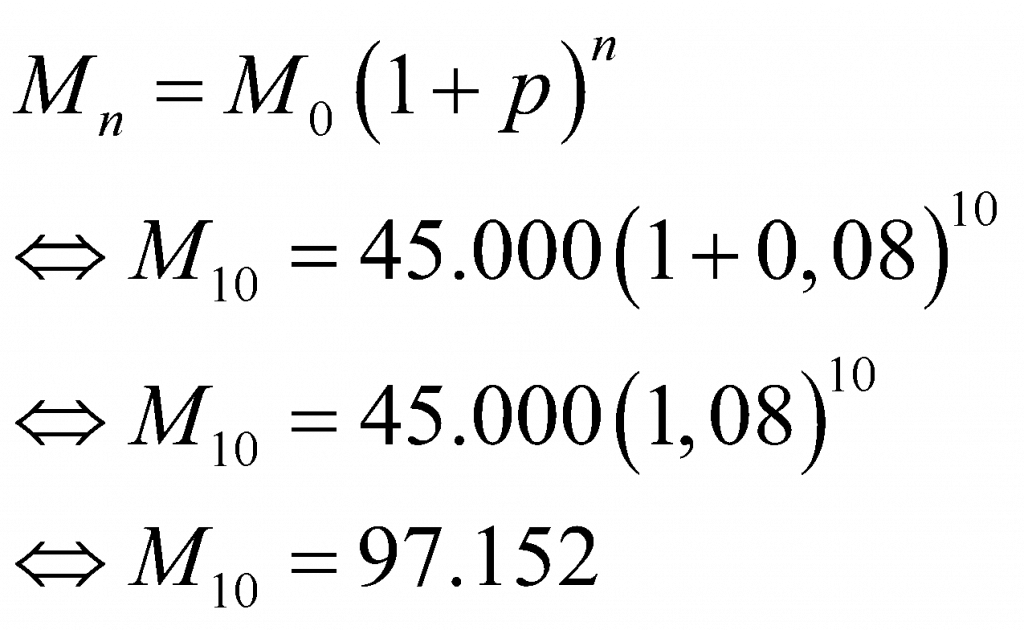
Terakhir, tentukan perbandingan antara M0 : M10.
M0 : M10
45.000 : 97.152
5.625 : 12.114
Jadi, perbandingannya adalah 5.625 : 12.114.
3. Contoh Soal 3
Seorang peneliti menyimpan 80 gram zat radioaktif. Karakteristik zat tersebut adalah akan meluruh 2% dari massa zat awalnya dalam waktu setiap 48 jam. Berapakah massa zat yang tersisa setelah 20 hari?
Pembahasan:
Diketahui:
M0 = 80 gram
p = 2% = 0,02
Oleh karena zat meluruh setiap 48 jam sekali = 2 hari sekali, maka n = 20 : 2 = 10.
Ditanya: M10 =…?
Jawab:
Untuk menentukan massa zat yang tersisa selama 20 hari, gunakan persamaan berikut.
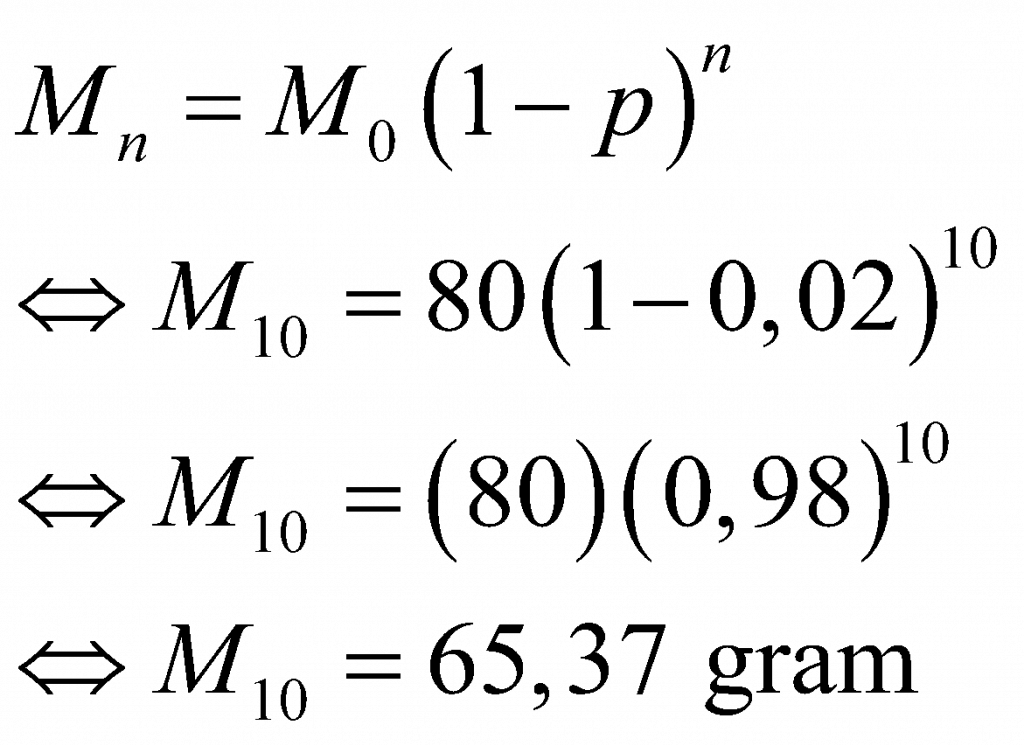
Jadi, massa zat radioaktif yang tersisa setelah 20 hari adalah 65,37 gram.
4. Contoh Soal 4
Pada tahun 2004, jumlah penduduk di kota A adalah 10.000. Menurut data sensus, angka kelahiran di kota A adalah 1,5% dari total penduduk yang ada di setiap periode. Berapakah jumlah penduduk kota A pada tahun 2010?
Pembahasan:
Diketahui:
M0 = 10.000 (jumlah penduduk pada tahun 2004 dijadikan sebagai acuan tahun setelahnya)
Tahun pertumbuhan (n) = 2005 – 2010 = 6 tahun
p = 1,5%
Ditanya: M6 =…?
Jawab:
Untuk menentukan jumlah penduduk tahun 2010, gunakan persamaan berikut.
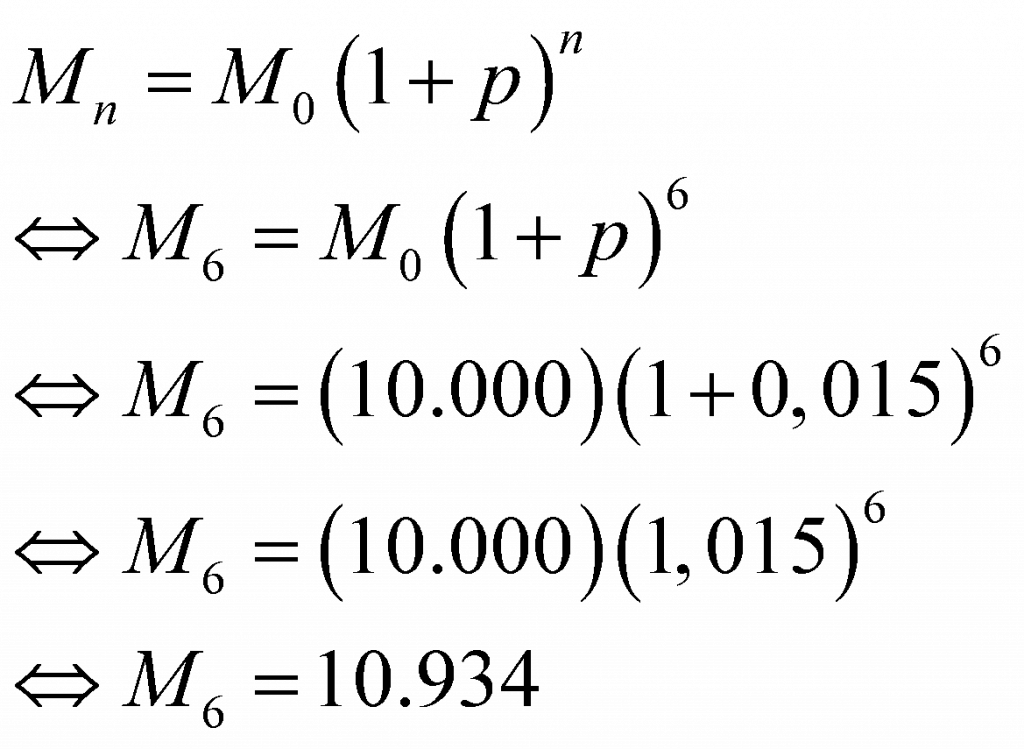
Jadi, jumlah penduduk kota A tahun 2010 adalah 10.934.
5. Contoh Soal 5
Harga penjualan mobil bekas selalu mengalami penurunan setiap tahunnya. Berdasarkan informasi dari sebuah showroom, bahwa penurunan itu bisa mencapai 2,5% per tahun, dengan ketentuan penurunan tersebut dihitung dari harga jual tahun sebelumnya. Jika harga mobil X pada tahun 2022 adalah Rp115.000.000, berapakah harga jual mobil tersebut pada tahun 2030?
Pembahasan:
Diketahui:
p = 2,5% = 0,025
M0 = Rp115.000.000
n = 2023 – 2030 = 8 tahun = 8
Ditanya: M8 =…?
Jawab:
Untuk menentukan harga jual mobil tahun 2030, gunakan persamaan penurunan berikut.
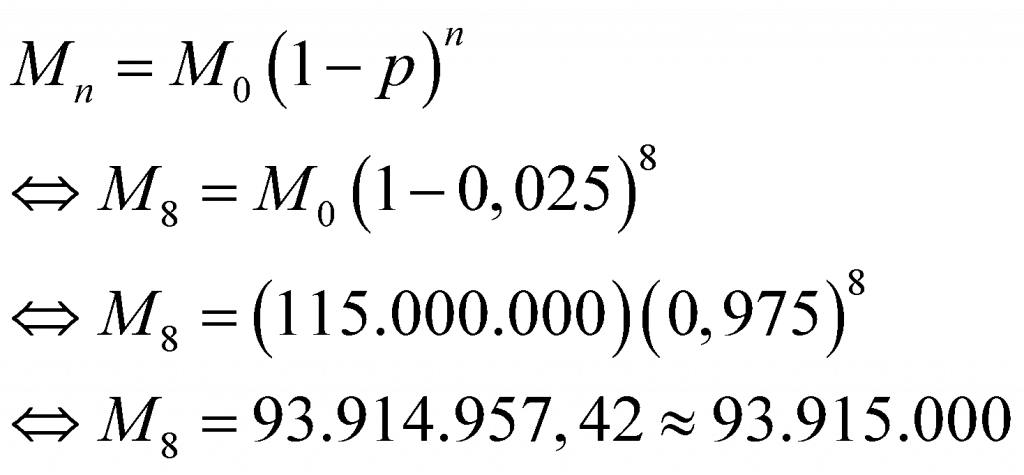
Jadi, harga jual mobil X pada tahun 2030 diperkirakan hanya Rp93.915.000.
6. Contoh Soal 6
Usopp menabungkan uang miliknya sejumlah Rp50.000.000 ke Bank Santika. Bank Santikamenentukan rasio bunga sebesar 8% setiap 6 bulan. Berapa tabungan Usopp bila waktu sudah berjalan selama 3 tahun?
Jawaban:

7. Contoh Soal 7
Abraham telah menabung selama 6 tahun di perbankan swasta yang bernama Bam Bank. Bila ketentuan bunga majemuk Bam Bank adalah 5% setiap caturwulan (4 bulan) sedangkan saldo awal Abraham berjumlah Rp10.000.000, maka berapakah saldo Abraham saat ini!
Jawaban:

8. Contoh Soal 8
Contoh soal 8 ini merujuk pada contoh soal 7 di atas. Berdasarkan data dari contoh soal 7 tersebut, apabila ketentuan bunga majemuk Bam Bank adalah 5% dengan periode setiap 3 bulan sekali, maka berapakah total bunga yang diterima Abraham?
Jawaban:

9. Contoh Soal 9
Agar dapat memenuhi impiannya, Sanji berusaha berinvestasi dalam bentuk tabungan. Sanji telah menabung uang sebesar Rp1.000.000.000 miliknya di Bloom Bank. Jika Bloom Bank memberi bunga majemuk sebesar 16% setiap tahun, dengan lamanya periode bunga majemuk tersebut adalah 3 bulan, berapakah total tabungan Sanji setelah 5 tahun?
Jawaban:

10. Contoh Soal 10
Berdasarkan informasi dari contoh soal 9 di atas, jika saldo awal Sanji hanya Rp500.000.000 maka berapakah total saldo akhirnya setelah 5 tahun?
Jawaban:

