Jenis-jenis Tumbukan dan Rumusnya

Tumbukan adalah peristiwa dua buah benda yang bergerak dengan kecepatan konstan, saling mendekati dan berinteraksi satu sama lain kemudian saling menjauh dengan kecepatan yang berbeda dengan kecepatan semula.

Setiap dua benda yang bertumbukan akan memiliki tingkat kelentingan atau elastisitas yang dinyatakan dengan koefisien restitusi ( e ).

Koefisien restitusi sendiri didefinisikan sebagai nilai negatif dari perbandingan kecepatan relatif sesudah tumbukan dengan kecepatan relatif sebelumnya.

Berdasarkan nilai koefisien restitusi, ada tiga jenis tumbukan yaitu tumbukan lenting sempurna, tumbukan lenting sebagian, dan tumbukan tidak lenting sama sekali.

1. Tumbukan Lenting Sempurna

Tumbukan lenting sempurna adalah tumbukan dua benda yang tidak mengakibatkan hilangnya energi kinetik. 

Pada tumbukan lenting sempurna berlaku hal-hal berikut.

• Berlaku Hukum Kekekalan Momentum dan Hukum Kekekalan Energi Kinetik.
• Jumlah momentum setelah tumbukan dan sebelum tumbukan adalah sama.
• Energi kinetik total kedua benda setelah tumbukan dan sebelum tumbukan adalah tetap. 
• Kecepatan setelah tumbukan sama yang ditentukan dari nilai e dan hukum kekekalan momentum. 
• Tumbukan lenting sempurna memiliki koefisien restitusi satu atau e = 1.

Karena tumbukan lenting sempurna memenuhi Hukum Kekekalan Momentum dan Hukum Kekekalan Energi Kinetik, rumusnya adalah sebagai berikut.

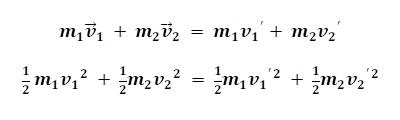
Contoh Soal :

Sebuah benda yang mula-mula diam ditumbuk oleh benda lain. Bila massa kedua benda sama dan tumbukan lenting sempurna, maka …

• setelah tumbukan, kecepatan benda yang menumbuk menjadi nol dan benda kedua kecepatannya sama dengan benda pertama sebelum menumbuk.
• koefisien restitusinya satu.
• jumlah momentum linear kedua benda sebelum dan sesudah tumbukan sama besar
• sebelum dan sesudah tumbukan, jumleh energi knetik kedua benda itu sama besar

Penyelesaian :

Sebelum tumbukan :

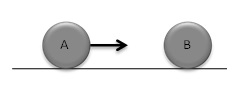
Setelah tumbukan :

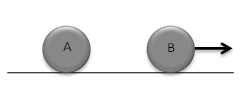
• EA + EB = EA’ + EB’
  ½ mvA² + ½ mvB² = ½ mvA’² + ½ mvB’²
  ½ mvA² = ½ mvB’²
  VA = VB’ maka kecepatan A sama besar kecepatan B setelah tumbukan…. (benar)
• Lenting sempurna e = 1 … (benar)
• Jumlah momentum linear kedua benda sebelum dan sesudah tumbukan sama besar (benar)
• Dari persamaan ½ mvA² = ½ mvB’² dapat dikatakan bahwa sebelum dan sesudah tumbukan jumlah energi kinetik kedua benda itu sama besar (benar).

2. Tumbukan Lenting Sebagian

Tumbukan lenting sebagian adalah tumbukan dua benda atau lebih yang memenuhi Hukum Kekekalan Momentum tetapi tidak berlaku Hukum Kekekalan Energi Kinetik.

Pada tumbukan lenting sebagian berlaku hal-hal berikut.

• Energi kinetik sebelum tumbukan lebih besar daripada energi kinetik setelah tumbukan karena sebagian energi kinetik setelah tumbukan berubah bentuk menjadi energi lain.  
• Tumbukan lenting sebagian memiliki memiliki koefisien restitusi antara nol dan satu atau 0 < e < 1.

Adapun derajat berkurangnya kecepatan relatif benda setelah tumbukan dirumuskan sebagai berikut.

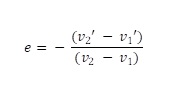
Contoh Soal :

Sebuah bola tenis dilepas dari ketinggian 200 m, jatuh mengenai lantai sehingga terjadi lenting sebagian. Hitunglah tinggi pemantulan pertama yang dapat dicapai oleh bola tenis (e = 0,2)

Penyelesaian :

Diketahui :
h₁ = 200 m
e = 0,2

Ditanyakan : h₂ = …?

Jawab :

Besar kecepatan bola memenuhi persamaan gerak jatuh bebas yaitu v = √2gh. Karena kecepatan lantai sebelum dan sesudah tumbukan sama dengan nol dan arah ke benda diberi harga negatif maka persamaannya adalah sebagai berikut.

Jadi, tinggi bola setelah memantul adalah 8 m.

3. Tumbukan Tidak Lenting Sama Sekali

Tumbukan tidak lenting sama sekali adalah tumbukan dua benda yang memenuhi Hukum Kekekalan Momentum tetapi tidak berlaku Hukum Kekekalan Energi Kinetik.

Pada tumbukan tidak lenting sama sekali berlaku hal-hal berikut.

• Setelah terjadi tumbukan, kedua benda  menyatu dan bergerak bersama-sama dengan kecepatan yang sama
• Jumlah energi kinetic sebelum tumbukan lebih besar daripada setelah tumbukan karena sebagian besar energi kinetiknya berubah bentuk
• Kecepatan kedua benda setelah tumbukan besarnya sama.
• Koefisien restitusi ( e ) adalah nol atau e = 0. 

Pada tumbukan tidak lenting sama sekali berlaku persamaan berikut.

m1v1 + m2v2 = m1v’1 + m2v’2 

Jika v’₁ = v’₂ = v’, maka persamaannya menjadi seperti berikut.

m1v1 + m2v2 = (m1 + m2) v’

Contoh Soal :

Dua buah benda A dan B massanya masing-masing 7 kg dan 5 kg bergerak berlawanan arah pada bidang licin dengan kelajuan sama 4 m/s. Jika terjadi tumbukan tidak lenting sama sekali, berapakah kecepatan kedua benda sesaat setelah tumbukan?

Penyelesaian :

Diketahui :
m_A = 7 kg
m_B  =5 kg
v_A = 4 m/s
v_B =-4 m/s (arah berlawanan)

Ditanya : v_A ‘ = …

Jawab:

m₁v₁ + m₂v₂ = (m₁ + m₂) v’
(7 x 4) + (5 x (-4)) = (7 + 5) v’
28 – 20 = 12v’
8 = 12v’
v’ = 0,67 m/s

Jadi kecepatan kedua benda sesaat setelah tumbukan adalah sebesar 0,67 m/s.