Pada pembahasan kali ini, kita akan membahas mengenai matriks yang meliputi pengertian matriks, operasi pada matriks dan yang pasti contoh soal dan pembahasannya agar membuat Anda semakin mengerti mengenai matriks.
Materi matriks dipelajari saat kita menduduki kelas X untuk yang menggunakan kurikulum 2013 dan kelas XII untuk yang masih menggunakan kurikulum KTSP. Simak dibawah ini pembahasan mengenai matriks.
Pengertian Matriks
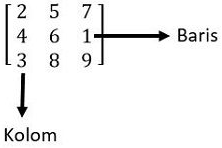
Matriks adalah kumpulan bilangan yang tersusun berdasarkan baris dan kolom dan berada diantara ada dua tanda kurung baik itu tanda kurung biasa ataupun tanda kurung siku. Bilangan yang ada pada matriks disebut dengan elemen matriks.
Elemen matriks dapat etrsusun secara vertikal (kolom) ataupun horizontal (baris).
Biasanya persoalan matematika yang menggunakan matriks yaitu mencari nilai persamaan linear, transformasi linear ataupun fungsi linear.
Misalkan untuk suatu matriks yang mempunyai m sebagai baris dan n sebagai kolom maka ditulis m x n atau bisa disebut matriks dengan ordo m x n.
Operasi Hitung Pada Matriks
1. Penjumlahan Matriks
Syarat dari penjumlahan suatu matriks yaitu memiliki ordo yang sama. Cara menjumlahkannya yaitu dengan menambahkan elemen yang mempunyai posisi sama, misalkan baris 1 kolom 1 matriks A ditambah dengan baris 1 kolom 1 matriks B.
2. Pengurangan Matriks
Syarat dari pengurangan suatu matriks sama dengan penjumlahan matriks yaitu memiliki ordo yang sama.
Cara menguranginya yaitu dengan mengurangi elemen yang mempunyai posisi sama, misalkan baris 1 kolom 1 matriks A dikurangi dengan baris 1 kolom 1 matriks B.
Untuk perkalian matriks ada dua yaitu :
- Perkalian matriks dengan bilangan real.
Untuk perkalian matriks dengan bilangan real, Anda dapat langsung mengalikan bilangan real tersebut dengan masing-masing elemen yang ada pada matriks tersebut,
- Perkalian dua matriks
Syarat dari perkalian dua matriks yaitu banyaknya kolom matriks A harus sama dengan banyak baris pada matriks.
Untuk perkalian dua buah matriks ada beberapa hal yang harus Anda ketahui yaitu:
- Tidak bersifat komutatif
- Bersifat Distributif = A * ( B + C ) = AB + AC
- Bersifat Asosiatif = A * (B * C) = (A*B) * C

4. Transpose Matriks
Transpose matriks adalah matriks yang ditulis dengan cara membalikkan baris menjadi kolom ataupun kolom menjadi baris.
5. Determinan Matriks
Determinan matriks dinotasikan | A | .
Untuk menentukan determinan matriks, ordo 2 x 2 dan ordo 3 x 3 berbeda. Untuk ordo 2 x 2 dengan cara kali silang lalu dikurangi.
Sedangkan untuk ordo 3 x 3 dengan menambahkan baris dan kolom baru lalu sama seperti ordo 2 dikali silang dan dikurangi.
6. Invers Matriks
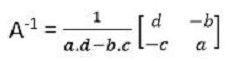
Invers suatu matriks dinotasikan A-1 , matriks yang mempunyai determinan 0 maka matriks tersebut tidak mempunyai invers.
Contoh Soal dan Pembahasan

Berikut ini akan di berikan beberapa contoh soal serti yang bisa anda lihat pada gambar di samping ini dan bisa anda jadikan panduan dalam mengerjakan, dibawah ini soal yang akan di bahas
1. Contoh soal dan pembahasan penjumlahan matriks.
Diketahui dua buah matriks, hitunglah :
A + B dan A - B
Ada bisa memahami soal yang tertera dengan memperhatikan gambar yang ada.
2. Diketahui sebuah matriks A.

Hitunglah 2A !
Untuk perkalian bilangan real, Anda langsung kalikan saja bilangan real dengan elemen pada matriks.
Seperti pada pembahasan disamping 2 dikalikan dengan 5, 2 dikalikan dengan 6 dan seterusnya.
3. Diketahui dua buah matriks. Matriks A dan Matriks B

Hitunglah AB!
Untuk perkalian dua buah matriks, yang dikalikan yaitu baris dikalikan kolom
Seperti pada pembahasan disamping baris kali kolom
A11 x B11 + A12 x B21 dan seterusnya.
4. Hitung determinan dari Matriks A pada soal no 2
|A| = 5.4 - 6.8 = 20 -48 = -28
5. Diketahui Matriks

Jika A = B tentukan x + y + z!
4 = 2y y = 4 /2 y = 2 x = 6 9 = 3z z = 9/3 z = 3
Maka x + y + z = 6 + 2 + 3 = 11


