Daftar isi
Matematika merupakan salah satu ilmu pengetahuan yang sangat populer dan menjadi pelajaran yang rumit buat beberapa orang.
Perkalian Matriks menjadi salah satu bahasan yang sering muncul dalam matematika.
Apa itu Perkalian Matriks?
Perkalian Matriks merupakan suatu operasi bilangan biner yang bisa menentukan matriks dan penentuan didasarkan 2 matriks yang berbeda pada suatu medan tertentu atau dalam suatu gelanggang.
Secara umum dalam dunia pendidikan disebutkan bahwa produk dari matriks dibuat untuk bisa menunjukkan atau menampilkan komposisi peta secara linier yang akan diwakili oleh berbagai matriksnya.
Dalam bidang aljabar linier, operasi matriks menjadi hal yang sangat mendasar.
Perkalian Matriks menjadi operasi bilangan yang sangat berhubungan dengan fisika, teknik dan cabang ilmu matematika.
Perkalian Matriks sangatlah penting untuk dipelajari, karena sangat berguna buat kehidupan sehari-hari.
Adapun jenis-jenis matrik, ialah:
- Matriks Persegi
Matriks persegi yaitu suatu matriks yang punya banyak baris dan jumlah kolom yang sama. Pada dasarnya matriks persegi memiliki ordo n x n. - Matriks Kolom
Matriks kolom yaitu suatu matriks yang hanya terdiri dari satu kolom saja dan matriks kolom biasanya memiliki ordo m x 1. - Matriks Bari
Matriks Baris yaitu suatu matriks yang hanya terdiri dari satu baris saja dan matriks baris biasanya memiliki ordo 1 x n. - Matriks Transpose
Matriks Transpose merupakan suatu matriks yang memiliki ordo n x m dan semua baris di dalamnya merupakan kolom-kolom matriks Am x n. - Matriks Diagonal
Matriks Diagonal merupakan matriks yang berasal dari matriks persegi dan matriks ini biasanya disebut dengan matriks diagonal, ketika semua elemen atau unsurnya selain elemen diagonal utamanya yaitu nol. - Matriks Segitiga Atas dan Bawah
Matriks segitiga atas & matriks segitiga bawah merupakan matriks-matriks yang bisa bersumber atau berasal dari matriks persegi. Matriks segitiga atas terbentuk saat semua elemen yang ada di bawahnya memiliki nilai nol. Sedangkan matriks segitiga bawah terbentuk saat semua elemen yang ada di atasnya memiliki nilai nol. - Matriks Simetri
Matriks Simetri merupakan matriks yang terbentuk saat adanya elemen pada suatu matriks yanng letaknya simetris terhadap diagonal utama dan bernilai sama. - Matriks Nol
Matriks nol merupakan matriks yang terbentuk saat semua elemen matriks bernilai nol. - Matriks Identitas
Matriks identitas yaitu suatu matriks diagonal yang semua elemen pembentuknya berada pada diagonal 1 dan pada dasarnya matriks identitas selalu dinotasikan dengan angka 1.
Sifat Perkalian Matriks
- Komutatif untuk penjumlahan yaitu A + B = B + A
- Assosiatif untuk penjumlahan yaitu (A + B) + C = A + ( B + C)
- Matriks nol yaitu A + 0 = A
- Lawan matriks yaitu A + (-A) = 0
- Asoasiatif untuk perkalian yaitu (AB) C = A (BC)
- Distributif kiri yaitu A(B + C) = AB + AC
- Distributif kanan yaitu (A+B) C = AC + BC
- Perkalian menggunakan konstanta yaitu k(AB) = (kA)B = A (kB), dimana k konstanta real
- Perkalian menggunakan matriks satuan yaitu AI = IA = A.
Rumus Perkalian Matriks
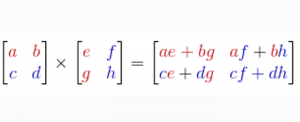
Pada dasarnya dalam kumpulan rumus matematika disebutkan, bahwa perkalian matriks menggunakan suatu metode rumus yang berbeda dengan berbagai perhitungan nilai pengurangan ataupun penjumlahan matriks.
Metode rumus memiliki fungsi dalam matematika yaitu sebagai perhitungan perkalian dalam bilangan matriks yaitu memakai baris pertama di matriks dengan dipadukan dengan kolom yang kedua di suatu matriks.
Secara umum kedua nilai matriks memang bisa dikalikan, saat jumlah kolom pertama dengan baris kedua sama.
Perkalian bilangan matriks akan menghasilkan baris yang sama dengan baris matriks yang awal atau pertama.
Contoh Soal Perkalian Matriks
Contoh Soal 1

Contoh Soal 2

