Sudut antara dua tali busur terbentuk dari dua buah tali busur yang berpotongan. Besar sudut antara dua tali busur nantinya bisa ditentukan dengan berdasarkan sifat-sifat segiempat tali busur ataupun menggunakan sifat sudut pusat dan sudut keliling.
Sebelum membahas terlalu jauh mengenai cara penentuan besar sudut antara dua tali busur, kita akan mengenal dahulu jenis-jenis dari perpotongan tali busur.
Dua tali busur dapat berpotongan pada dua kondisi yaitu berpotongan di dalam lingkaran dan juga berpotongan di luar lingkaran. Kedua kondisi ini masing-masing akan menghasilkan sudut dengan ukuran tertentu.
1. Sudut antara Dua Tali Busur Berpotongan di Dalam Lingkaran
Dua tali busur yang berpotongan di dalam lingkaran akan membentuk sudut. Agar lebih memahami mengenai jenis sudut ini maka perhatikan gambar berikut.
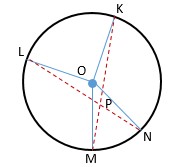
Pada gambar di atas, terdapat lingkaran berpusat di O dengan titik P merupakan titik potong antara busur KM dan busur LN. Perhatikan bahwa kedua busur KM dan busur LN memenuhi kondisi berpotongan di dalam lingkaran.
Dari perpotongan ini terbentuklah beberapa sudut, yaitu ∠KPL, ∠KPN, ∠LPM, dan ∠MPN. Keempat sudut ini adalah sudut antara dua tali busur yang berpotongan di dalam lingkaran.
Nah, sekarang bagaimana cara kita menentukan besar sudut antara dua tali busur yang berpotongan di dalam lingkaran? Untuk menjawabnya kita akan menggunakan garis bantuan. Misal akan ditentukan besar ∠MPN, maka kita akan menggunakan garis bantuan dari titik K dan titik N yaitu garis KN. Perhatikan gambar di bawah ini.
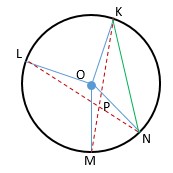
Dari garis bantu KN kita akan memperoleh ∠MKN = ∠PKN. Hal ini karena ∠MKN dan ∠PKN adalah sudut keliling yang menghadap busur MN. Coba perhatikan bahwa ada sudut lain yang menghadap busur MN yaitu sudut pusat MON. Berdasarkan sifat sudut pusat dan sudut keliling diperoleh,
∠MKN = ∠PKN = ½ × ∠MON …… (i)
Mari kita lihat sudut yang lain. Perhatikan sudut-sudut yang menghadap ke busur KL. Sudut-sudut tersebut adalah ∠KNL, ∠KNP, dan ∠KOL. Untuk ∠KNL dan ∠KNP adalah sudut keliling, dan ∠KOL adalah sudut pusat. Analog dengan cara untuk memperoleh persamaan (i) maka diperoleh,
∠KNL = ∠KNP = ½ × ∠KOL …… (ii)
Selanjutnya, perhatikan △KPN. Berdasarkan sifat jumlah sudut dalam segitiga diperoleh,
∠PKN + ∠KNP + ∠KPN = 1800
∠KPN = 1800 – ∠PKN – ∠KNP …… (iii)
Salah satu sudut luar △KPN adalah ∠MPN. Ada dua sudut yang saling berpelurus yaitu ∠MPN dan ∠KPN. Dengan menggunakan sifat sudut yang saling berpelurus maka,
∠MPN + ∠KPN = 1800
⇔ ∠MPN + (1800 – ∠PKN – ∠KNP) = 1800 {substitusikan pers (iii)}
⇔ ∠MPN = ∠PKN + ∠KNP
⇔ ∠MPN = (½ × ∠MON) + (½ × ∠KOL) {substitusikan pers (i) dan pers (ii)}
⇔ ∠MPN = ½ × (∠MON + ∠KOL)
Dengan menggunakan analogi dari cara di atas kita akan menentukan besar ∠LPM. Pertama-tama kita akan menggunakan garis bantuan dari titik K dan titik L yaitu garis KL. Perhatikan gambar di bawah ini.
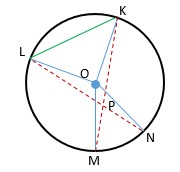
Dari garis bantu KN kita akan memperoleh ∠LKP = ∠LKM. Hal ini karena ∠LKP dan ∠LKM adalah sudut keliling yang menghadap busur LM. Coba perhatikan bahwa ada sudut lain yang menghadap busur LM yaitu sudut pusat LOM. Berdasarkan sifat sudut pusat dan sudut keliling diperoleh,
∠LKP = ∠LKM = ½ × ∠LOM …… (iv)
Mari kita lihat sudut yang lain. Perhatikan sudut-sudut yang menghadap ke busur KN. Sudut-sudut tersebut adalah ∠KLN, ∠KLP, dan ∠KON. Untuk ∠KLN dan ∠KLP adalah sudut keliling, dan ∠KON adalah sudut pusat. Analog dengan cara untuk memperoleh persamaan (iv) maka diperoleh,
∠KLN = ∠KLP = ½ × ∠KON …… (v)
Selanjutnya, perhatikan △KLP. Berdasarkan sifat jumlah sudut dalam segitiga diperoleh,
∠KLP + ∠LKP + ∠KPL = 1800
∠KPL = 1800 – ∠KLP – ∠LKP …… (vi)
Salah satu sudut luar △KPN adalah ∠LPM. Ada dua sudut yang saling berpelurus yaitu ∠LPM dan ∠KPL. Dengan menggunakan sifat sudut yang saling berpelurus maka,
∠LPM + ∠KPL = 1800
⇔ ∠LPM + (1800 – ∠KLP – ∠LKP) = 1800 {substitusikan pers (vi)}
⇔ ∠LPM = ∠KLP + ∠LKP
⇔ ∠LPM = (½ × ∠KON) + (½ × ∠LOM) {substitusikan pers (iv) dan pers (v)}
⇔ ∠LPM = ½ × (∠KON + ∠LOM)
Dengan menggunakan analogi cara yang sama untuk mendapatkan rumus ∠MPN dan ∠LPM, selanjutnya bisa ditentukan rumus untuk sudut ∠LPK dan ∠KPN. Sehingga dari kondisi perpotongan tali busur KM dan tali busur LN seperti pada gambar selanjutnya diperoleh rumus sebagai berikut.
∠MPN = ½ × (∠MON + ∠KOL) ∠LPM = ½ × (∠KON + ∠LOM) ∠KPL = ½ × (∠KOL + ∠MON) ∠KPN = ½ × (∠KON + ∠LOM)
Secara garis besar dapat ditarik sebuah kesimpulan bahwa “Besar sudut antara dua tali busur yang berpotongan di dalam lingkaran sama dengan setengah dari penjumlahan sudut-sudut pusat yang menghadap busur diapit oleh kaki-kaki sudut tersebut”.
2. Sudut antara Dua Tali Busur Berpotongan di Luar Lingkaran
Tali busur lingkaran juga bisa berpotongan di luar lingkaran. Perpotongan ini diperoleh dengan membuat perpanjangan dari dua tali busur jika kedua tali busur tersebut tidak berpotongan di dalam lingkaran. Untuk lebih jelasnya coba perhatikan gambar berikut.
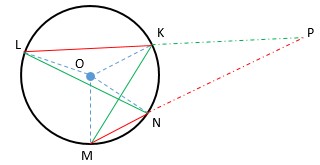
Pada lingkaran dengan pusat O di atas, terdapat tali busur KL dan MN. Juga terdapat 4 sudut pusat yaitu ∠KOL, ∠LOM, ∠MON, dan ∠KON. Tali busur KL dan MN tidak berpotongan di dalam lingkaran sehingga kedua tali busur ini diperpanjang hingga berpotongan di luar lingkaran yaitu pada titik P. Dari hasil perpotongan kedua tali busur ini terbentuklah ∠KPN.
Perhatikan sudut keliling yang menghadap busur KN yaitu ∠KMN, dan sudut pusat yang menghadap busur KN yaitu ∠KON. Karena kedua sudut pusat dan sudut keliling ini menghadap busur yang sama maka berlaku ∠KMN = ½ × ∠KON.
Selanjutnya, perhatikan sudut keliling yang menghadap busur LM yaitu ∠LKM, dan sudut pusat yang menghadap busur LM yaitu ∠LOM. Dari kedua sudut ini berlaku ∠LKM = ½ × ∠LOM.
Pada △KPM, tinjaulah ∠LKM yang merupakan sudut luar △KPM. Dari kondisi ini diperoleh,
∠LKM = ∠KMN + ∠KPN
⇔ ∠KPN = ∠LKM – ∠KMN
Karena sebelumnya sudah diperoleh kondisi ∠KMN = ½ × ∠KON dan ∠LKM = ½ × ∠LOM, sehingga
⇔ ∠KPN = (½ × ∠LOM) – (½ × ∠KON)
⇔ ∠KPN = ½ × (∠LOM – ∠KON)
Jadi dapat ditarik sebuah kesimpulan bahwa “Besar sudut antara dua tali busur yang berpotongan di luar lingkaran sama dengan setengah dari selisih sudut-sudut pusat yang menghadap busur yang diapit oleh kaki-kaki sudut tersebut”.
