Bangun Ruang Kubus : Unsur, Ciri Ciri, Rumus dan Contoh Soal

Kubus merupakan bangun ruang tiga dimensi yang mempunyai 6 buah sisi yang berbentuk persegi dengan panjang sisi yang sama. Contoh kubus dalam kehidupan sehari-hari adalah rubik, kado, kardus, dadu, dll.

Unsur unsur pada kubus:

• Sisi : sisi adalah bidang pada bangun ruang yang membatasi bangun ruang dengan ruangan di sekitarnya

• Rusuk : Rusuk adalah garis potong antara 2 sisi kubus, yang terlihat seperti kerangka penyusun kubus. Rusuk pada gambar kubus disamping yaitu, AB, BD, DC, CA, EF, FG, GH, HE, AE, BF, CH, dan GD

• Titik Sudut : Titik sudut adalah titik potong antara dua buah sudut

• Diagonal Bidang : Diagonal bidang adalah garis yang menghubungkan antara titik sudut yang berhadapan pada setiap sisi kubus.

• Diagonal Ruang : Diagonal ruang adalah ruas garis yang menghubungkan titik sudut yang berhadapan dalam suatu ruang pada kubus.

• Bidang Diagonal : Bidang diagonal adalah bidang yang dibatasi oleh rusuk dan diagonal bidang pada kubus

Ciri Ciri Kubus

Kubus mempunyai ciri-ciri :

1. Memiliki 6 buah sisi yang sama berbentuk persegi
2. Memiliki 8 buah titik sudut
3. Memiliki 12 buah rusuk yang sama panjang
4. Memiliki 12 buah diagonal bidang yang sama panjang
5. Memiliki 4 buah diagonal ruang yang sama panjang
6. Memiliki 6 buah bidang diagonal, yang berbentuk persegi panjang saling kongruen

[accordion]
[toggle title=”Matematika Dasar”]

• Pengertian Bilangan Bulat
• Pengertian Himpunan
• Pengertian Bilangan Prima
• Rumus Bangun Datar
• Pengertian Bilangan Komposit

[/toggle]

[toggle title=”Rumus”]

• Rumus Peluang
• Rumus Luas dan Keliling Segitiga
• Rumus Aljabar

[/toggle]
[/accordion]

Rumus Kubus

Rumus pada bidang ruang kubus meliputi rumus luas permukaan, volume, diagonal bidang, diagonal ruang, bidang diagonal, panjang rusuk kubus.

(berdasarkan gambar kubus diatas)

Luas permukaan = luas ABCD + luas EFGH + luas ABFE + luas CDGH + luas ACEH + luas BDFG

= ( s x s ) + ( s x s ) + ( s x s ) + ( s x s ) + ( s x s ) + ( s x s )

= 6 x  s²

Volume = sisi x sisi x sisi

= sisi³

[AdSense-A]

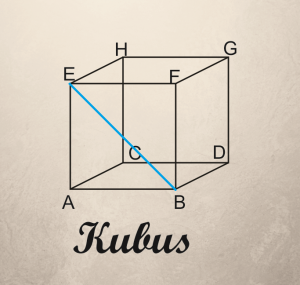Diagonal bidang:

Panjang BE pada gambar disamping dapat dihitung dengan rumus pythagoras.

BE = akar dari (AE² + AB²)

BE = akar dari (sisi² + sisi²)

BE = akar dari 2 x sisi²

BE = sisi akar dari 2

Diagonal ruang:

Pada gambar di samping, BH merupakan diagonal ruang. Selain BH, ada juga AG, CF, dan DE.

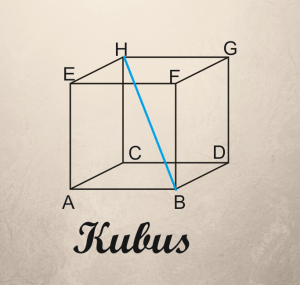
Untuk mencari panjang BH sama seperti pada diagonal bidang menggunakan rumus pythagoras.

BH = akar dari (BC² + CH²)

BH = akar dari (sisi akar 2)² + sisi²)

BH = akar dari (2 x sisi² ) + sisi²

BH = akar dari (3 x sisi²)

Contoh Soal dan Pembahasan

1.Sebuah kubus memiliki panjang sisi 14 cm hitunglah luas permukaan dan volumenya!

jawab : Luas permukaan = 6 x sisi ²

= 6 x 14²

= 6 x 14 x 14 = 1.176 cm²

Volume = sisi x sisi x sisi

= 14 x 14 x 14

=  2.744 cm³

2. Sebuah kubus memiliki panjang rusuk 6cm, hitunglah diagonal bidang, diagonal ruang, dan luas salah satu bidang diagonalnya!

jawab : Panjang diagonal bidang = sisi √ 2

= 6 √2 cm

Panjang diagonal ruang = sisi √3

                                                   = 6 √3 cm

Luas bidang diagonal = sisi²√2 

                                             =(6 cm)²√2

                                             = 36√2 cm² 

[AdSense-C]

3. Diketahui volume sebuah kubus ada 343 cm^3, berapakah panjang sisi dan jumlah panjang rusuk kubus tersebut!

volume = 343 cm³

volume = sisi x sisi x sisi

343 = sisi x sisi x sisi

sisi = 3√343

       = 7 cm

4. Hajaj akan memberikan hadiah sebanyak 64 jam tangan yang dikemas dalam kontak berbentuk kubus yang mempunyai sisi 3cm. Jam tangan tersebut akan di masukkan kedalam kardus yang berbentuk kubus lebih besar. Berapa panjang kotak kardus besar yang akan digunakan?

jawab :

volume kardus besar = 64

r kardus besar =   3√64

                              = 4 x 3 cm

                              = 12 cm

Sekian penjelasan mengenai materi kubus, semoga contoh soal dan pembahasan dapat membantu dalam menyelesaikan tugas anda.